Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 4.Exercícios - Ex. 99

Um caminhão de entregas viaja do ponto A   ao ponto   B e volta usando a mesma rota, todos os dias. Existem quatro semáforos no caminho. Sejam X 1 o número de faróis vermelhos que o caminhão encontra quando vai de A para B e X 2 , o número encontrado quando ele retorna. Os dados coletados durante um longo período sugerem que a distribuição de probabilidade conjunta é dada por

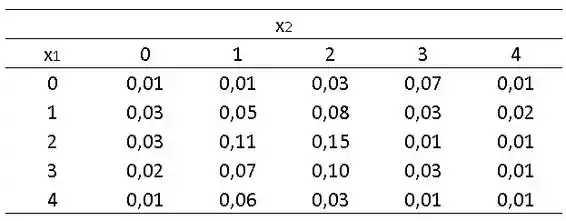
(a) Dê a densidade marginal de X 1 .

(b) Dê a densidade marginal de X 2 .

(c) Dê a distribuição de densidade condicional de X 1 dado que X 2 = 3 .

(d) Dê E ( X 1 ) .

(e) Dê E ( X 2 ) .

(f) Dê E X 1 X 2 = 3 .

(g) Dê o desvio-padrão de X 1 .

Passo 1

Falaa, meu querido/minha querida. A densidade marginal de uma variável aleatória discreta X 1 é dada por:

g x 1 = ∑ x 2 f ( x 1 ,   x 2 )

Para a variável X 2 , temos:

h x 2 = ∑ x 1 f ( x 1 ,   x 2 )

Então, bora para os cálculos!!!

Passo 2

Usando a tabela e a fórmula que definimos no Passo 1, temos:

g 0 = f 0 ,   0 + f 0 ,   1 + f 0 ,   2 + f 0 ,   3 + f 0 ,   4

= 0,01 + 0,01 + 0,03 + 0,07 + 0,01 = 0,13

g 1 = f 1 ,   0 + f 1 ,   1 + f 1 ,   2 + f 1 ,   3 + f 1 ,   4

= 0,0 3 + 0,0 5 + 0,0 8 + 0,0 3 + 0,0 2 = 0 , 21

g 2 = f 2 ,   0 + f 2 ,   1 + f 2 ,   2 + f 2 ,   3 + f 2 ,   4

= 0,0 3 + 0 , 1 1 + 0 , 15 + 0,0 1 + 0,01 = 0 , 31

g 3 = f 3 ,   0 + f 3 ,   1 + f 3 ,   2 + f 3 ,   3 + f 3 ,   4

= 0,0 2 + 0,0 7 + 0 , 10 + 0,0 3 + 0,01 = 0 , 2 3

g 4 = f 4 ,   0 + f 4 ,   1 + f 4 ,   2 + f 4 ,   3 + f 4 ,   4

= 0,01 + 0,0 6 + 0,03 + 0,0 1 + 0,01 = 0,1 2

Passo 3

De forma similar a letra (a), a distribuição marginal de X 2 é:

h 0 = f 0 ,   0 + f 1 ,   0 + f 2 ,   0 + f 3 ,   0 + f 4 ,   0

= 0,01 + 0,03 + 0,03 + 0,02 + 0,01 = 0,10

h 1 = f 0 ,   1 + f 1 ,   1 + f 2 ,   1 + f 3 ,   1 + f 4 ,   1

= 0,01 + 0,0 5 + 0 , 11 + 0,0 7 + 0,0 6 = 0 , 3 0

h 2 = f 0 ,   2 + f 1 ,   2 + f 2 ,   2 + f 3 ,   2 + f 4 ,   2

= 0,0 3 + 0,0 8 + 0 , 15 + 0 , 10 + 0 , 03 = 0 , 39

h 3 = f 0 ,   3 + f 1 ,   3 + f 2 ,   3 + f 3 ,   3 + f 4 ,   3

= 0,0 7 + 0,03 + 0,0 1 + 0,0 3 + 0,01 = 0,1 5

h 4 = f 0 ,   4 + f 1 ,   4 + f 2 ,   4 + f 3 ,   4 + f 4 ,   4

= 0,01 + 0,0 2 + 0,0 1 + 0,0 1 + 0,01 = 0 , 06

Passo 4

Nós precisamos encontrar os valores de f ( x 1 | 3 ) para todos os valores de x 1 . Lembrando que a fórmula é:

f x 1 3 = f ( x 1 , 3 ) h ( 3 )

Sendo assim, temos os seguintes valores:

f 0 3 = f ( 0,3 ) h ( 3 ) = 0,07 0,15 = 7 15

f 1 3 = f ( 1 , 3 ) h ( 3 ) = 0,0 3 0,15 = 3 15

f 2 3 = f ( 2 , 3 ) h ( 3 ) = 0,0 1 0,15 = 1 15

f 3 3 = f ( 3 , 3 ) h ( 3 ) = 0,0 3 0,15 = 3 15

f 4 3 = f ( 4 , 3 ) h ( 3 ) = 0,0 1 0,15 = 1 15

Passo 5

Agora, queremos encontrar o valor esperado da variável X 1 , e a fórmula para isso é:

E X 1 = ∑ x 1 x 1 g x 1

= 0 0,13 + 1 0,21 + 2 0,31 + 3 0,23 + 4 0,12

E X 1 = 2

Passo 6

Encontrando o valor esperado para X 2 :

E X 2 = ∑ x 2 x 2 g x 2

= 0 0,10 + 1 0,30 + 2 0,39 + 3 0,15 + 4 0,06

E X 2 = 1,77

Passo 7

Usando os resultados que encontramos no Passo 4, o valor esperado é:

E X 1 X 2 = 3 = ∑ x 2 x 1 f x 1 3

= 0 7 15 + 1 1 5 + 2 1 15 + 3 1 5 + 4 1 15

E X 1 X 2 = 3 = 1,2

Passo 8

Por fim, precisamos determinar o desvio-padrão de X 1 , então, vamos encontrar a variância:

σ X 1 2 = ∑ x 2 x 1 - E X 1 2 g X 1 = ∑ x 2 x 1 - 2 2 g X 1

= 0 - 2 2 0,13 + 1 - 2 2 0,21 + 2 - 2 2 0,31 + 3 - 2 2 0,23 + 4 - 2 2 0,12

σ X 1 2 = 1,44

Como o desvio-padrão é a raiz quadrada da variância:

σ X 1 = 1,44 = 1,2

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

Um sinal consiste numa série de vibrações de magnitude X, tendo os valores –1, 0, 1, cada um com probabilidade 1/3. Um ruído consiste numa série de vibrações, de magnitude Y, tendo osvalores –2, 0, 2,
Sabe-se, por meio da coleta de dados e de muitas pesquisas, que o tempo, em segundos, que certo funcionário de uma empresa chega atrasado para o trabalho é a variável aleatória X , com função de densi
O lucro de um revendedor com um novo automóvel, em unidades de $ 5.000, é a variável aleatória X , que tem como função de densidade f x = 2 1 - x , 0 ≤ x ≤ 1 0 , c a s oc o n t r á r i o á (a) Determi
Uma loja de conveniência tem dois locais separados em que os clientes fecham a conta antes de ir embora. Ambos os locais têm duas caixas registradoras e dois funcionários para fechar a conta dos clien