Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 4.Exercícios - Ex. 100

Uma loja de conveniência tem dois locais separados em que os clientes fecham a conta antes de ir embora. Ambos os locais têm duas caixas registradoras e dois funcionários para fechar a conta dos clientes. Sejam X o número de caixas registradoras usadas em um momento específico no local 1 e Y , o número de caixas registradoras usadas no mesmo período no local 2. A função de probabilidade conjunta é dada por

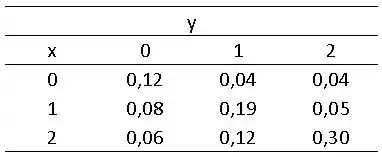
(a) Dê as densidades marginais de X e Y bem como a distribuição de probabilidade de X dado que Y = 2 .

(b) Dê E ( X ) e V a r ( X ) .

(c) Dê E ( X | Y = 2 ) e V a r ( X | Y = 2 ) .

Passo 1

Falaa, meu querido/minha querida. A densidade marginal de uma variável aleatória discreta X é dada por:

g x = ∑ y f ( x ,   y )

Para a variável Y , temos:

h y = ∑ x f ( x ,   y )

Então, bora para os cálculos!!!

Passo 2

Usando a tabela e a fórmula que definimos no Passo 1, temos:

g 0 = f 0 ,   0 + f 0 ,   1 + f 0 ,   2 = 0,12 + 0,04 + 0,04 = 0,20

g 1 = f 1 ,   0 + f 1 ,   1 + f 1 ,   2 = 0 , 08 + 0 , 19 + 0,0 5 = 0 , 32

g 2 = f 2 ,   0 + f 2 ,   1 + f 2 ,   2 = 0 , 06 + 0 , 12 + 0 , 30 = 0 , 48

Para a variável aleatória Y , temos:

h 0 = f 0 ,   0 + f 1 ,   0 + f 2 ,   0 = 0,12 + 0,0 8 + 0,0 6 = 0 , 26

h 1 = f 0 ,   1 + f 1 ,   1 + f 2 ,   1 = 0 , 04 + 0 , 19 + 0 , 12 = 0 , 35

h 2 = f 0 ,   2 + f 1 ,   2 + f 2 ,   2 = 0 , 04 + 0,0 5 + 0 , 30 = 0 , 39

Nós precisamos encontrar os valores de f ( x | 2 ) para todos os valores de x . Lembrando que a fórmula é:

f x 2 = f ( x , 2 ) h ( 2 )

Sendo assim, temos os seguintes valores:

f 0 2 = f ( 0 , 2 ) h ( 2 ) = 0,0 4 0 , 39 = 4 39

f 1 2 = f ( 1 ,   2 ) h ( 2 ) = 0,0 5 0 , 39 = 5 39

f 2 2 = f ( 2 ,   2 ) h ( 2 ) = 0 , 30 0 , 39 = 30 39

Passo 3

Agora, o enunciado nos pede o valor esperado de X :

E X = ∑ x x g ( x )

= 0 0,2 + 1 0,32 + 2 ( 0,48 )

E X = 1,28

E a variância que é calculada da seguinte forma:

V X = ∑ x x - E X 2 g ( X ) = ∑ x x - 1,28 2 g ( X )

= 0 - 1,28 2 0,20 + 1 - 1,28 2 0,32 + 2 - 1,28 2 0,48

V X = 0,602

Passo 4

Por fim, queremos encontra o valor esperado e a variância de X dado que Y = 2 .

O valor esperado é definido por:

E X Y = 2 = ∑ x x f ( x | 2 )

= 0 4 39 + 1 5 39 + 2 30 39

E X Y = 2 = 5 3

E a variância é:

V a r X Y = 2 = ∑ x x - E X Y = 2 2 f x 2

= 0 - 5 3 2 4 39 + 1 - 5 3 2 5 39 + 2 - 5 3 2 30 39

V a r X Y = 2 = 50 117

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

Suponha que você jogue um dado, não adulterado, de dez lados (0, 1, 2, ..., 9) 500 vezes. Usando o teorema de Chebyshev, calcule a probabilidade de que a média amostral, X , esteja entre 4 e 5.
Prove o teorema de Chebyshev quando X for umavariável aleatória discreta.
Considere o Exercício 4.10. Pode-se dizer que as notas dadas pelos dois especialistas são independentes? Explique.
Um importante sistema age como apoio para um veículo do programa espacial. Um componente único e crucial opera somente 85% do tempo. Para aumentar a confiabilidade no sistema, decidiu-se que três comp
Nos negócios é importante planejar e realizar pesquisas para antecipar o que ocorrerá no final do ano. Pesquisas sugerem que o espectro de lucro (perda) seja o que se segue, com as respectivas probabi