Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 30
Um sinal consiste numa série de vibrações de magnitude X, tendo os valores –1, 0, 1, cada um com probabilidade 1/3. Um ruído consiste numa série de vibrações, de magnitude Y, tendo os
valores –2, 0, 2, com probabilidades 1/6, 2/3, 1/6, respectivamente. Combinando-se o sinal com o ruído, obtemos o sinal efetivamente observado, Z = X + Y. Construa a função de probabilidade para Z e calcule a sua média e variância, admitindo que sinal e ruído são independentes..
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para pegar o que aconteceu lá na combinação das variáveis e encontrar a esperança e a variância. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser construir uma tabela com todos os dados que ele falou no enunciado.
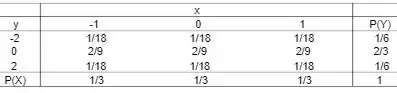
Agora que já temos tudo arrumadinho bonitinho na tabela, podemos ver os valores certos para o nosso cálculo da esperança e da variância.
Passo 3
Pronto!! Agora é só calcular a esperança e a variância!!