Num certo ano, foi feito um levantamento, em 10 estados brasileiros, a respeito do número de vagas oferecidas nas escolas de nível superior (), em 1.000 unidades, em função do número de candidatos aprovados () e do número de candidatos inscritos ().
Efetuando os cálculos dos somatórios necessários ao cálculo de regressão, foram obtidos:

Pede-se:
- Testar a existência da regressão múltipla, ao nível de 0,5%.
Passo 1
Olá galerinha, tudo bem com vocês? Vem comigo!
A regressão linear múltipla é a regressão em que sabemos como variáveis contribuem para a realização do fenômeno, e a parte funcional da regressão é uma função linear. Onde a estimativa da equação de regressão é dada por:
Onde as estimativas , , , , dos coeficientes , , , , podem ser calculadas pelo método dos mínimos quadrados, partindo de hipóteses análogas aquelas adotadas pela regressão linear simples.
Para fazermos o teste de existência da regressão múltipla, iremos faze pela Análise de Variância representada pela tabela:
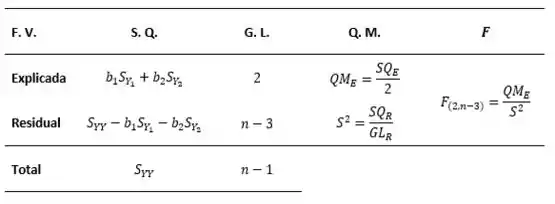
Se existe regressão de sobre e .
Passo 2
Então vamos lá! Do exercício 6c, temos os seguintes dados:
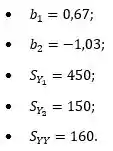
Primeiramente iremos encontrar nosso tabelado, onde:
- ;
- .
Para :
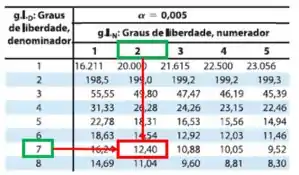
Passo 3
O cálculo das somas dos quadrados:
Completando nossa tabela de Análise de Variância:
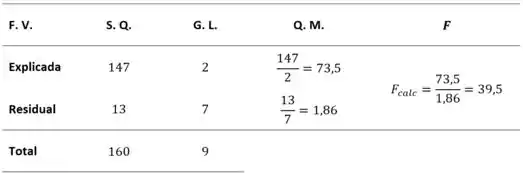
Como (), então existe regressão de sobre e .
Prontinho pessoal, até mais!
Resposta
Existe regressão ().