Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 14.Exercícios propostos - Ex. 9e
Foi feito o levantamento, com pessoas, a respeito da idade , em função da respectiva altura (em cm) e do respectivo peso (em kg).
Efetuando os cálculos dos somatórios necessários à montagem de regressão, obtivemos:
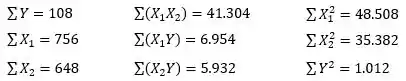
Pede-se:
- Testar a existência da regressão múltipla e efetuar a análise de seu melhoramento (em relação à regressão simples só com ), ambas ao nível de 2,5%.
Passo 1
Olá galerinha, tudo bem com vocês? Primeiramente iremos relembrar a teoria.
A regressão linear múltipla é a regressão em que sabemos como variáveis contribuem para a realização do fenômeno, e a parte funcional da regressão é uma função linear. Onde a estimativa da equação de regressão é dada por:
Onde as estimativas , , , , dos coeficientes , , , , podem ser calculadas pelo método dos mínimos quadrados, partindo de hipóteses análogas aquelas adotadas pela regressão linear simples.
Para fazermos o teste de existência da regressão múltipla e análise de melhoramento, iremos fazer pela Análise de Variância representada pela tabela:
- Se existe regressão de sobre e ;
- Se o melhoramento é significativo para essa variável .
Para a análise de melhoramento em relação a :
Passo 2
Então vamos lá! Do exercício 9b), temos os seguintes dados:
- ;
- ;
- ;
- ;
- ;
- .
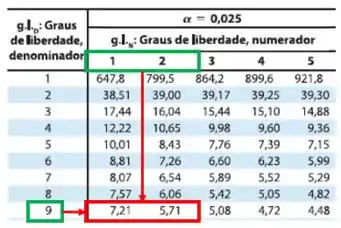
Antes de iniciarmos iremos encontrar o tabelado, para os dois testes, onde:
- ;
- ;
- .
Para :
Passo 3
Então agora vamos calcular os quadrados médios:
Como (), então existe regressão de sobre e .
Passo 4
Agora vamos calcular o melhoramento:
Como (), o melhoramento não é significativo em relação a para .
Espero ter conseguido te ajudar, até mais!
Resposta
Existe regressão ();
O melhoramento não é significativo ().