Certo tipo de câmera digital é oferecido em duas versões de três megapixel e quatro megapixel. Uma loja de câmeras recebeu uma encomenda de 15 dessas câmeras, das quais seis com resolução de três megapixel. Suponha que cinco delas sejam selecionadas aleatoriamente para serem estocadas atrás do balcão. As outras 10 são colocadas na área de armazenagem. Seja X número de câmeras de três megapixel entre as cinco selecionadas para armazenagem atrás do balcão. a. Que tipo de distribuição tem X (nome e valores de todos os parâmetros)? b. Calcule P(X 2), P(X 2) e P(X 2). c. Calcule o valor médio e o desvio padrão de X.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
DEFINIÇÕES
Fórmula probabilidade hipergeométrica:
Regra de adição para eventos disjuntos ou mutuamente exclusivos:
Passo 2
- Estamos interessados no número de sucessos entre um número fixo de tentativas de uma população finita, que tem uma distribuição
- Avalie a definição de probabilidade hipergeométrica em x=0,1,2:
- A média de uma distribuição hipergeométrica é o produto do número de sorteios e o número de sucessos observados, dividido pelo tamanho da população:
Passo 3
Use a regra de adição para eventos mutuamente exclusivos:
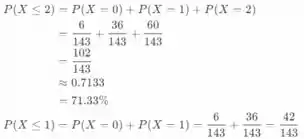
Use a regra do complemento:
A variância da distribuição hipergeométrica é
O desvio padrão é a raiz quadrada da variância:
Resposta
Ver o desenvolvimento