Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 2.Exercícios - Ex. 161
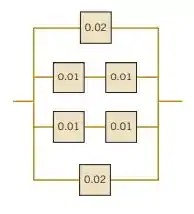
O circuito a seguir opera se, e somente se, houver um caminho de dispositivos funcionais de esquerda para a direita. Considere que os dispositivos falhem independentemente e que a probabilidade de falha de cada equipamento esteja mostrada na figura. Qual é a probabilidade de o circuito não operar?
Passo 1
Vamos denotar os ramos do circuito, de cima para baixo, como e . Então podemos definir os números para como probabilidades de falha do i-ésimo ramo.
As falhas dos dispositivos são mutuamente independentes, assim como as falhas dos ramos. Portanto, a probabilidade de um circuito não operar é:
Passo 2
Agora, vamos calcular usando a regra da independência e a regra geral de adição para 2 eventos:
Substitua isso em para obter o resultado final:
Resposta
Exercícios de Livros Relacionados
Três dados são rolados. Supondo que cada um dos 63 = 216 resultados possíveis seja igualmente provável, determine as probabilidades associadas aos valores possíveis que X pode assumir, onde X é a soma
No Problema 4.5, para n= 3 , se a moeda é honesta, quais são as probabilidades associadas aos valores que X pode assumir?
Um vendedor agendou duas visitas para vender enciclopédias. Sua primeira visita resultará em venda com probabilidade 0,3, e sua segunda visita resultará em venda com probabilidade de 0,6, sendo ambas
No jogo de morra dois dedos dois jogadores mostram um ou dois dedos e dizem simultaneamente o número de dedos que o seu oponente irá mostrar. Se apenas um dos jogadores acertar ele recebe uma quantida
Cinco números distintos são aleatoriamente distribuídos entre jogadores numerados de 1 a 5. Sempre que dois jogadores comparam os seus números, aquele com o maior número é declarado vencedor. Inicialm