Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 3.2 - Ex. 37
Confiabilidade do teste - Um certo vírus infecta uma em cada 200 pessoas. Um teste usado para detectar o vírus em uma pessoa dá positivo 80% das vezes quando a pessoa tem o vírus e 5% das vezes quando a pessoa não tem o vírus. (Este resultado de 5% é chamado de falso positivo.) Seja A o evento “a pessoa está infectada” e B o evento “o teste dá positivo”
(a) Usando o teorema de Bayes, se o teste dá positivo, determine a probabilidade de a pessoa estar infectada.
(b) Usando o teorema de Bayes, se o teste dá negativo, determine a probabilidade de a pessoa não estar infectada.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Vamos primeiro fazer uma árvore de probabilidades, no enunciado da questão diz que o vírus infecta uma em cada 200 pessoas, e o teste dá positivo em 80% dos casos quando a pessoa é portadora do vírus, com isso, nós temos que
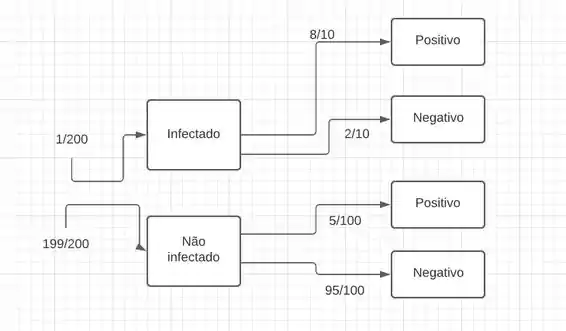
A – Utilizando o teorema de Bayes, nós temos o seguinte equacionamento
Fazendo a substituição, nós temos que
Que nos dá como resultado
Passo 2
B – Para o caso do teste dá negativo e a pessoa não esteja infectado, nós temos que
Fazendo a substituição dos valores, nós temos que
Com isso, nós temos o seguinte resultado