Exercícios de Teorema de Bayes - Lista de Exercícios Resolvida

Numa certa região, a probabilidade de chuva em um dia qualquer de primavera é de 0,1. Um meteorologista da TV acerta suas previsões em 80 dos dias em que chove e em 90% dos dias em que não chove.

a. Qual é a probabilidade do meteorologista acertar sua previsão?

b. Se houve acerto na previsão feita, qual a probabilidade de ter sido um dia de

chuva?

Três candidatos disputam as eleições para o Governo do Estado. O candidato do partido de direita tem 30 da preferência eleitoral, o de centro tem 30 e o da esquerda 40. Em sendo eleito, a probabilidade de dar, efetivamente, prioridade para Educação e Saúde é de 0,4; 0,6 e 0,9 para os candidatos de direita, centro e esquerda, respectivamente.

(a) Qual é a probabilidade de não ser dada prioridade a essas áreas no próximo governo?

(b) Se a área teve prioridade, qual a probabilidade do candidato de direita ter ganho a eleição?

A chance do barco “Da Noi" vencer uma regata se o vento estiver forte (acima de 20 nós) é de 80% e de 40% se o vento estiver fraco. No dia da regata, a meteorologia prevê vento forte com 70% de chance. Qual a probabilidade de:

1. “Da Noi" vencer a regata?
2. O vento ter sido forte sabendo que “Da Noi" venceu a regata?
3. O vento ter sido fraco sabendo que “Da Noi" não venceu a regata?

Sabe-se que dos minérios de uma pequena região encontram-se em localidades de difícil acesso. Nas localidades mais acessíveis (que não são de difícil acesso), apenas dos minérios tem valor comercial. Nas localidades de difícil acesso, pesquisadores estimam que dos minérios tenham valor de comércio.

1. Qual é o percentual de minérios com algum valor comercial em toda a região, considerando como correta a estimativa dos pesquisadores?
2. Qual é a probabilidade de que um minério sorteado ao acaso tenha vindo de uma localidade de difícil acesso dado que é um minério com valor comercial?
3. Desconsiderando a estimativa dos pesquisadores, qual deve ser a real proporção de minérios com valor comercial nas localidades de difícil acesso para que a dificuldade de acesso e o valor comercial do minério sejam independentes do ponto de vista probabilístico.

Suponha que tenhamos 5 dados em uma caixa. 4 são balanceados, mas em um deles a probabilidade de ocorrer face “seis” é o quádrulo da probabilidade de ocorrer outra face. As faces restantes têm igual probabilidade de ocorrer. Um desses dados é selecionado ao acaso e é lançado. Qual é a probabilidade de esse dado ser balanceado se sair “seis”?

Uma revista deseja estudar o comportamento do mercado brasileiro especificamente para clientes interessados em carros japoneses das marcas T Toyota), H (Honda) e N (Nissan). A compra do primeiro carro é feita com as probabilidades ; e . Um estudo sobre os hábitos de mudança de marca por parte dos usuários mostrou o seguinte quadro de probabilidades condicionais que prevalece em qualquer momento no qual um usuário típico adquire um novo automóvel:

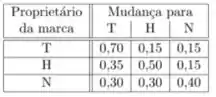
Por exemplo, representa mudança de um carro da marca Toyota no momento para outro carro Toyota no momento . Sendo assim, olhando na tabela, temos por exemplo , e para todo .

Quais são as probabilidades de que, para um tal cliente:

a) O segundo automóvel seja um Toyota, ou seja ? De que seja Honda, ou seja, ? De que seja Nissan, ou seja, ?

b) O terceiro automóvel seja um Toyota, ou seja, ?

c) O primeiro automóvel tenha sido um Toyota, dado que o segundo também foi da marca Toyota, isto é, ?

Três companhias aéreas servem uma pequena cidade no estado de São Paulo. As companhias , e tem, respectivamente e de voos programados. As taxas de voos que saem no horário programado são e , respectivamente.

1. Um voo acaba de sair no horário programado. Qual é a probabilidade que seja da companhia ?
2. Qual é a probabilidade de um voo não ser da companhia ou não sair no horário programado?

Em um curso secundário, dos estudantes são do sexo masculino e dos estudantes são do sexo feminino. Entre os rapazes, 20% estudam ciências, enquanto entre as moças, apenas 10% dedicam-se às ciências. Obtenha as probabilidades de que:

1. um estudante escolhido ao acaso estude ciências;
2. um estudante de ciências selecionado ao acaso seja do sexo feminino.

A chance do barco “Da Noi" vencer uma regata se o vento estiver forte (acima de 20 nós) é de 80% e de 40% se o vento estiver fraco. No dia da regata, a meteorologia prevê vento forte com 70% de chance. Qual a probabilidade de:

1. “Da Noi" vencer a regata?
2. O vento ter sido forte sabendo que “Da Noi" venceu a regata?
3. O vento ter sido fraco sabendo que “Da Noi" não venceu a regata?

Uma urna contém 3 moedas onde uma tem duas caras, outra é uma moeda justa, e a terceira é uma moeda viciada com probabilidade de cara igual a 0,75. Uma moeda é selecionada aleatoriamente da urna e lançada uma vez, tendo se observado o resultado cara. Qual a probabilidade da moeda escolhida ter duas caras?

João dispõe de dois meios de transporte para se deslocar da cidade para a cidade B. Caso utilize o meio de transporte nº1, João chegará atrasado em das vezes; se utilizar o transporte nº2 chegará atrasado em das vezes (suponha que as chances de João utilizar os meios sejam: para o nº1 e para o nº2). Se João chegou atrasado num compromisso na cidade , qual a probabilidade de ter utilizado o transporte nº1 ?

Em uma determinada fábrica constatou-se em registros passados, que uma determinada máquina para a produção de parafusos funciona corretamente do tempo. Se a máquina não está funcionando corretamente, dos parafusos produzidos são defeituosos e quando a máquina estiver trabalhando corretamente, apenas dos parafusos são defeituosos. Pede-se:

1. Se um parafuso é escolhido aleatoriamente, qual é a probabilidade de que ele seja defeituoso?
2. Uma vez que o parafuso seja defeituoso, qual é a probabilidade de que este pertence a máquina que esteja funcionando corretamente.

Em uma determinada fábrica constatou-se em registros passados, que uma determinada máquina para a produção de parafusos funciona corretamente do tempo. Se a máquina não está funcionando corretamente, dos parafusos produzidos são defeituosos e quando a máquina estiver trabalhando corretamente, apenas dos parafusos são defeituosos. Pede-se:

1. Se um parafuso é escolhido aleatoriamente, qual é a probabilidade de que ele seja defeituoso?
2. Uma vez que o parafuso seja defeituoso, qual é a probabilidade de que este pertence a máquina que esteja funcionando corretamente.

A incidência de Câncer no pulmão causado pela poluição produzida na combustão de carvão é de caso por da população. Como informação adicional, sabe-se que de cada casos, são suaves e são crônicos.

Um novo instrumento detector desta doença está sendo testado. Sabe-se que este aparelho detecta o câncer no estado crônico com certeza, detecta o câncer no estado suave com probabilidade de e indica a presença da doença mesmo quando esta não existe com probabilidade de .

Avalie o desempenho deste aparelho na detecção correta da existência desta doença (nos estados suave e crônico) num paciente. Comente os resultados.

O receptor de um determinado equipamento de uma rede de telecomunicações recebe mensagens de instruções através de três possíveis transmissores diferentes. Estatísticas da rede mostram que 50% das mensagens recebidas são enviadas pelo transmissor 1, 40% pelo transmissor 2 e 10% pelo transmissor 3. Para fins de garantia de integridade das informações, o protocolo de comunicação exige que o receptor confirme o recebimento repetindo ao seu transmissor a mensagem recebida. Entretanto, a chance dos transmissores enviarem mensagens contendo erros nos bits que os identificam é de 1%, 3% e 6%, respectivamente. Com base nessas estatísticas, calcule:

1. A probabilidade de chegar uma mensagem no receptor com erro de identificação do remetente e, portanto, o receptor não ter certeza sobre qual transmissor ele deve responder.
2. Para cada um dos três transmissores, a probabilidade deste ter sido o remetente de uma mensagem que chegou no receptor com erro na identificação.

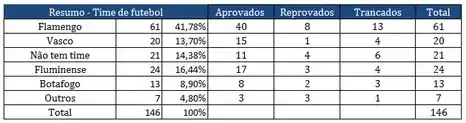
A disciplina PROBEST é obrigatória para a conclusão de vários cursos de graduação do CTC da PUC. No quadro abaixo, apresenta-se o resultado desta disciplina relativo aos alunos matriculados na matéria PROBEST no período passado.

Baseando neste quadro e usando o teorema de BAYES, pede-se:

1. Qual a probabilidade de um aluno ter que repetir (reprovados + trancados) a disciplina PROBEST?
2. Dado que o aluno vai repetir a disciplina, qual a probabilidade do aluno torcer para o time de futebol “Flamengo”.

Admita que, em determinada localidade, se um trabalhador do comércio ficar desempregado, a probabilidade de que ele consiga um novo emprego similar dentro de 6 meses é de 0,6. Caso contrário (com probabilidade 0,4), ele abre seu próprio negócio. Sabe-se também que, tendo conseguido um novo emprego assalariado, em 5% das vezes sua família troca as crianças de colégio. Já os que montam seu próprio negócio trocam suas crianças de colégio em 15% das vezes. Se neste local for selecionado um trabalhador do comércio recém-desempregado:

a)Qual a probabilidade de que suas crianças mudem de escola?

b)Dado que as crianças de fato trocaram de escola, qual a probabilidade de que ele tenha conseguido um novo emprego?

Uma empresa de desenvolvimento urbano considera a possibilidade de construir um shopping center num setor no Rio de Janeiro. Um elemento vital é uma proposta em um setor com estrada que liga ao centro da cidade.

Se o Conselho aprovar essa rodovia, há probabilidade de de a empresa construir o shopping, enquanto, se a rodovia não for aprovada a probabilidade é de apenas . Com base em informações disponíveis, o presidente da empresa estima uma chance de de que a estrada seja aprovada.

Pergunta-se:

a) Qual é a probabilidade de a empresa construir o shopping? Mostre o evento correspondente através do Diagrama de Venn (partição do espaço amostral).

b) Uma vez que o shopping foi construído, qual é a probabilidade de que a rodovia não seja aprovada?

Um trabalhador pediu a seu supervisor uma carta de recomendação para um novo emprego. Ele estima que há 80% de chances de que obtenha o trabalho se receber uma excelente (E) recomendação, 40% de chance se a recomendação for moderadamente boa (M), e 10% de chance se a recomendação for fraca (F). Pelo que o trabalhador conhece da avaliação do supervisor, ele ainda estima que as probabilidades da recomendação ser excelente(E), moderada(M) e fraca(F) são 70%, 20%, e 10%, respectivamente. Calcule a probabilidade:

(a) de que ele vá receber a oferta de trabalho (T);

(b) da recomendação ter sido Excelente, Moderada e Fraca dado que ele tenha recebido a oferta de trabalho;

(c) da recomendação ter sido Excelente, Moderada e Fraca dado que ele não tenha recebido a oferta de trabalho;

(d) As probabilidades originais de , , e , respectivamente estimadas para recomendação ser excelente(E), moderada(M) e fraca(F) foram alteradas nos itens (b) e (c) ora para mais, ora para menos em função do resultado que elas produziram. Como você explica a lógica destas modificações?

Um engenheiro apresentou orçamentos separados para a execução de uma obra num prédio em construção. O primeiro orçamento foi feito para a parte elétrica do prédio e o segundo orçamento foi feito levando em consideração a parte de encanamento do edifício. O engenheiro acha que a probabilidade de ganhar a concorrência da parte elétrica é de . Caso ele ganhe a parte elétrica, a chance de ganhar a parte de encanamento é de ; caso contrário, essa probabilidade é de . O engenheiro gostaria de saber qual a probabilidade:

(a) de ganhar o contrato referente à parte de encanamento;

(b) de ganhar os dois contratos;

(c) de ganhar apenas um contrato;

(d) condicional de ganhar o contrato da parte elétrica, dado que já ganhou o da parte de encanamento.

Sabe-se que dos minérios de uma pequena região encontram-se em localidades de difícil acesso. Nas localidades mais acessíveis (que não são de difícil acesso), apenas dos minérios tem valor comercial. Nas localidades de difícil acesso, pesquisadores estimam que dos minérios tenham valor de comércio.

1. Qual é o percentual de minérios com algum valor comercial em toda a região, considerando como correta a estimativa dos pesquisadores?
2. Qual é a probabilidade de que um minério sorteado ao acaso tenha vindo de uma localidade de difícil acesso dado que é um minério com valor comercial?
3. Desconsiderando a estimativa dos pesquisadores, qual deve ser a real proporção de minérios com valor comercial nas localidades de difícil acesso para que a dificuldade de acesso e o valor comercial do minério sejam independentes do ponto de vista probabilístico.

Uma empresa de desenvolvimento urbano considera a possibilidade de construir um shopping Center num setor no Rio de Janeiro. Um elemento vital é uma proposta em um setor com estrada que liga ao centro da cidade. Se o Conselho aprovar essa rodovia, há probabilidade de da empresa construir o shopping, enquanto, se a rodovia não for aprovada a probabilidade é de apenas . Com base em informações disponíveis, o presidente da empresa estima que uma chance que a estrada seja aprovada.

Pergunta-se:

1. Qual é a probabilidade da empresa construir o shopping?
2. Uma vez que o shopping foi construído, qual é a probabilidade de que a rodovia seja aprovada?

Em uma determinada fábrica constatou-se em registros passados, que uma determinada máquina para a produção de parafusos funciona corretamente do tempo. Se a máquina não está funcionando corretamente, dos parafusos produzidos são defeituosos, e quando a máquina estiver trabalhando corretamente, apenas dos parafusos são defeituosos. Pede-se:

1. Se um parafuso é escolhido aleatoriamente, qual é a probabilidade de que ele não esteja defeituoso?
2. Uma vez que o parafuso não esteja defeituoso, qual é a probabilidade de que este pertence a máquina que esteja funcionando corretamente.

Observação: utilize o teorema de Bayes.

Uma fábrica de televisores compra 1/5 de transistores que necessita de um fornecedor que garante uma confiabilidade (probabilidade de funcionar corretamente sem defeitos) de 80% ao seu material durante um certo período. A aquisição do restante material é igualmente dividida por duas outras firmas que garantem, respectivamente, confiabilidades de 85% e 95% durante o mesmo período de tempo.

b) Para cada um dos fornecedores, determine a probabilidade de que o transistor escolhido ao acaso do estoque tenha sido comprado deste fornecedor sabendo-se que este transistor se revelou defeituoso, aplicando o Teorema de Bayes.

Observação: mostre os resultados considerando 4 casas decimais.

Em uma certa população foi constatado que a prevalência de diabetes é de . Um determinado teste diagnostica que, se o paciente não é sadio existe do resultado ser positivo, e, se o paciente não tem a doença existe de não detectar no teste.

Uma pessoa é diagnosticada. Qual é a probabilidade de que realmente ela está diabética, sabendo-se que o resultado do teste foi positivo (acusou a existência da doença)?

Em um país hipotético, 60% dos eleitores não possuem preferência partidária definida, 20% dos eleitores apoiam partidos de oposição e 20% apoiam partidos da situação. Admita que:

• Há independência entre ter ou não preferência partidária definida e aprovar ou não o governo atual;

• Entre os eleitores que apoiam partidos de oposição, todos desaprovam o governo;

• Entre os eleitores que apoiam partidos da situação, 75% aprovam o governo.

(a) Qual é a proporção dos eleitores que aprovam o governo?

(b) Dado que um eleitor aprova o governo, qual é a probabilidade condicional: De que ele não tenha preferência partidária definida? De que apoie um partido de oposição? De que apoie um partido da situação?

(c) Dado que um eleitor não aprova o governo, qual é a probabilidade condicional: De que não tenha preferência partidária definida? De que apoie um partido de oposição? De que apoie um partido da situação?

Uma fábrica de televisores compra 2/5 de transistores que necessita de um fornecedor que garante uma confiabilidade (probabilidade de funcionar corretamente sem defeitos) de 80% ao seu material durante um certo período.

A aquisição do restante material é igualmente dividida por duas outras firmas que garantem, respectivamente, confiabilidades de 60% e 70% durante o mesmo período de tempo. Pede-se:

1. Seleciona-se ao acaso um transistor do estoque da fábrica para o teste. Qual a probabilidade dele funcionar corretamente? Mostre o evento correspondente através do Diagrama de Venn (partição do espaço amostral).
2. Qual a origem mais provável de um transistor que escolhido ao acaso do estoque, se verificou ter funcionado mal?

Observação: utilize o teorema de Bayes.

Há três urnas numa sala. A urna possui bolas vermelhas e brancas; a urna possui bolas vermelhas e brancas; a urna possui bolas vermelhas e brancas. A urna é selecionada ao acaso e duas bolas são retiradas. Uma vez que as duas bolas são vermelhas, qual a probabilidade da urna ter sido selecionada?