Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 102
Considere a descrição do exercício 9-101. Depois de coletar uma amostra, estamos interessados em testar, com. Para cada uma das situações seguintes, calcule o valor P para esse teste:
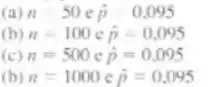
e) comente sobre o efeito do tamanho da amostra sobre o valor P verdadeiro observado do teste.
Passo 1
Estamos interessados em testar
Contra:
O valor P para isso é a probabilidade acima de mais a probabilidade abaixo. Porque a distribuição normal padrão é simétrica em torno de zero, uma simples maneira de escrever isso é:
Passo 2
Letra a:
Sabemos que a média da amostra é n = 50 e 0,095. A estatística de teste é
Do que da primeira equação e da Tabela III do Apêndice, obtemos o valor P:
Passo 3
Letra b:
Sabemos que a média da amostra é n = 100 e p = 0.005. Da mesma maneira que na parte a) nós temos
e
Passo 4
Letra c:
Sabemos que a média da amostra é n = 500 e p= 0,095. Da mesma maneira que
na parte a) nós temos
e
Passo 5
Letra d:
Nós sabemos que a média da amostra é n = 1000 e p = 0.095. Da mesma maneira que
na parte a) nós temos
e
Passo 6
Letra e:
Se o tamanho da amostra aumentar, o valor P diminui.
Resposta
- -0.12, e
- -0.17 e
- -0.37 e
- -0.53 e
- Se o tamanho da amostra aumentar, o valor P diminui.