Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 100

Suponha que desejamos testar a hipótese H 0 : μ = 85 verus H 1 : μ > 85 em que σ = 16 . Suponha que a média verdadeira seja μ = 86   e que, no contexto prático do problema, isso não constitui um desvio de que tem importância prática.

  1. Para um teste com α = 0.01 , calcule β para tamanhos de amostra de n=25, 100, 400 e 2500, supondo que μ = 86 .
  2. Suponha que a média amostral seja x _ = 86 . Encontre o valor P para estatística de teste, para os diferentes tamanhos de amostra especificados no item a. Os dados seriam estatisticamente significante se α = 0.01 ?
  3. Comente o uso de um tamanho grande de amostra neste problema.

Passo 1

Queremos testar a hipótese

H 0 :   μ = 85   v e r s u s   H 1 : μ > 85 ,

onde σ = 16 e a média verdadeira é 86.

Ao avaliar o procedimento de teste de hipóteses, também é importante examinar a probabilidade de um erro do tipo II. Isso é

β = P ( f a l h a   e m   r e j e i t a r   H 0   q u a n d o   H 0   é   f a l s o ) = Φ ( z a - δ n σ )

onde, δ = μ - μ 0

Passo 2

Letra a:

Para um teste com α = 0.01 e δ = 86 - 85 = 1 , obtemos:

Para n = 25   o erro tipo 2 é

β = Φ ( 2.33 - 1 25 16 ) = Φ ( 2.02 ) = 0.978308

Para n = 100   o erro tipo 2 é

β = Φ ( 2.33 - 1 100 16 ) = Φ ( 1.705 ) = 0.955435

Para n = 400   o erro tipo 2 é

β = Φ ( 2.33 - 1 400 16 ) = Φ ( 1.08 ) = 0.859929

Para n = 2500   o erro tipo 2 é

β = Φ ( 2.33 - 1 2500 16 ) = Φ ( - 0.795 ) = 0.214764

Passo 3

Letra b:

A estatística de teste para este teste é

z 0 = x ̄ - μ σ / n = 86 - 85 16 / n = n 16

O valor P é o menor nível de significância que levaria à rejeição da hipótese nula H 0 com os dados fornecidos. Nesse caso, o valor P é:

P = 1 - Φ ( z 0 ) = 1 - Φ ( n 16 )

Agora, das equações anteriores, obtemos:

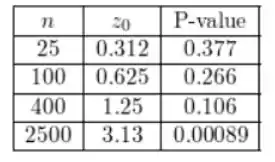
Em n = 2500, o valor P é menor que 0.01 e rejeitamos H 0 . Para determinar o valor exato dessa probabilidade, usamos a planilha do google e a função N O R M . S . D I S T ( x ; T R U E ) .

Passo 4

Letra c:

Quando o tamanho da amostra aumenta, o valor P diminui e β   aumenta.

Resposta

  1. n = 25 ,   β = 0.978

    2. n = 100 ,   β = 0.955

    n = 400 ,   β = 0.859

    n = 2500 ,   β = 0.215

  2. n = 25 ,   P v a l o r = 0.377

    3. n = 100 ,   P v a l o r = 0.266

    n = 400 ,   P v a l o r = 0.106

    n = 2500 ,   P v a l o r = 0.00089

  3. Quando o tamanho da amostra aumenta, o valor P diminui e β   aumenta.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para estudar o impacto de cenas violentas em desenhos animados, 5 crianças tiveram seus batimentos cardíacos medidos, antes e após assistirem a um desenho comercialmente veiculado por uma grande emiss
Deseja-se comparar a durabilidade de amortecedores fabricados pelas empresas A e B. A medida observada é o índice de resistência de cada peça testada em laboratório, que é assumido ter a mesma variabi
A sequência de operações executadas por um operário para realizar uma certa tarefa está sendo estudada. Para tanto, 9 operários foram sorteados e mediu-se o tempo necessário, em minutos, para que cada
Num programa de diminuição da poluição sonora em cidades grandes, realizou-se uma campanha educativa durante 2 meses. A tabela abaixo apresenta os índices alcançados antes e após a campanha de dez pon
O tempo de conexão a Internet tem sido modelado pela distribuição Normal com desvio padrão de 10 e 7 minutos para o público jovem e adulto, respectivamente. Amostras independentes desses dois grupos p