Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 5.Exercícios - Ex. 15
Considere um sistema formado por três componentes, conforme ilustração. O sistema continuará funcionando desde que o primeiro componente funcione e que o componente 2 ou o 3 funcionem também. Represente por , e os tempos de vida dos componentes 1, 2 e 3, respectivamente. Suponha que os s sejam independentes entre si e que cada possua uma distribuição exponencial com parâmetro .
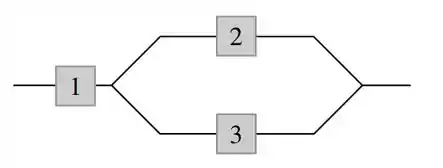
a. Seja tempo de vida do sistema. Obtenha a função de distribuição acumulada de e calcule a diferença para obter a fdp. [Sugestão: ; expresse o evento em termos de uniões e/ou interseções dos três eventos ,, e.]
b. Calcule a vida útil esperada do sistema.
Passo 1
Falaaa, meu querido/minha querida. Como vai?? Aqui, nossa variável aleatória é dada por:
Pois, o enunciado nos diz que temos uma distribuição exponencial com parâmetro Então, bora calcular o que o enunciado nos pede!!!
Passo 2
A função de densidade cumulativa da uma variável aleatória exponencialmente distribuída é:
,
A fdc de é:
Então, vamos encontrar essa probabilidade.
,
,
Portanto, a fdc de é:
Agora, a fdp de pode ser obtida derivando a função acima:
,
,
Sendo assim, a fdp de é definida por:
Passo 3
O valor esperado é a integral da fdp.
Então, para o nosso exemplo temos o seguinte:
Resposta
- Resolução no Passo 2.