Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 5.Exercícios - Ex. 13

Você tem duas lâmpadas para uma determinada luminária. Seja X vida útil da primeira lâmpada e Y vida útil da segunda lâmpada (ambas de mil horas). Suponha que X e Y   sejam independentes e que cada uma tenha distribuição exponencial com parâmetro λ = 1 .

a. Qual é a fdp conjunta de X e Y ?

b. Qual é a probabilidade de cada lâmpada durar no máximo 1000 horas (isso é, X ≤ 1   e   Y ≤ 1 ) ?

c. Qual é a probabilidade de a vida útil total das duas lâmpadas ser no máximo 2? [Sugestão: desenhe a região A = { ( x ,   y ) :   x ≥ 0 ,   y ≥ 0 ,   x + y ≤ 2 } antes da integração.]

d. Qual é a probabilidade de a vida útil total estar entre 1 e 2?

Passo 1

Falaaa, meu querido/minha querida. Como vai?? Aqui, nossa variável aleatória X é dada por:

f X x = λ e - λ x                                           x ≥ 0 0                                                               x < 0

Pois, o enunciado nos diz que temos uma distribuição exponencial com parâmetro λ .

Portanto, nós temos que:

f X x = e - x                                                     x ≥ 0 0                                                               x < 0

f Y y = e - y                                                     y ≥ 0 0                                                               y < 0

Então, bora calcular o que o enunciado nos pede!!!

Passo 2

Podemos notar que as variáveis são independentes. Portanto, a fdp conjunta é:

f x ,   y = f X x ∙ f Y y = e - x - y                                   x ≥ 0 ,   y ≥ 0 0                                         c a s o   c o n t r á r i o

Passo 3

Conforme o Passo 1, temos a seguinte probabilidade:

P X ≤ e   Y ≤ 1 = P ( X ≤ 1 ) ∙ P ( Y ≤ 1 )

= 1 - e - 1 ∙ 1 - e - 1

= 0,4

Passo 4

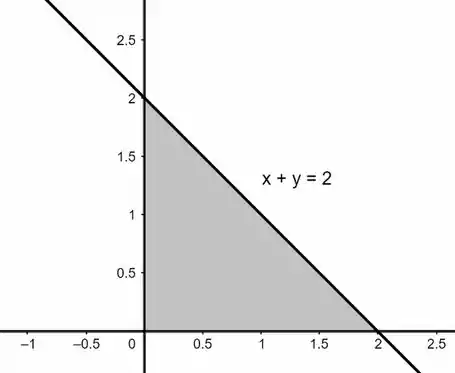
A partir da imagem acima, podemos perceber que a área que devemos integrar é:

P X + Y ≤ 2 = ∫ 0 2 ∫ 0 2 - x e - x e - y d y d x

= 1 - e - 2 - 2 e - 2

P X + Y ≤ 2 = 0,594

Passo 5

A probabilidade de a vida útil estar entre 1 e 2 é:

P 1 ≤ X + Y ≤ 2 = P X + Y ≤ 2 - P ( X + Y ≤ 1 )

= 0,594 - 0,264

P 1 ≤ X + Y ≤ 2 = 0,33

Resposta

  1. f x ,   y = e - x - y                                   x ≥ 0 ,   y ≥ 0 0                                         c a s o   c o n t r á r i o

  2. P X ≤ 1   e   Y ≤ 1 = 0,4

  3. P X + Y ≤ 2 = 0,594

  4. P 1 ≤ X + Y ≤ 2 = 0,33

Exercícios de Livros Relacionados

Na caixa I existem duas bolas numeradas 0 e 1, enquanto que a caixa II contêm duas bolas numeradas 1 e 0. Uma bola é retirada aleatoriamente de cada caixa, de forma independente uma da outra. A esse e
Na caixa I existem duas bolas numeradas 0 e 1, enquanto que a caixa II contêm duas bolas numeradas 1 e 0. Uma bola é retirada aleatoriamente de cada caixa, de forma independente uma da outra. A esse e
A variável X é Bernoulli com p :0,4 e Y é Binomial com p :0,5en :3 . Admita que XeY são independentes.Determine P X = 0 Y = 2 . Obtenha a função de probabilidade conjunta do X e Y e do produto XY.Calc
A variável X é Bernoulli com p :0,4 e Y é Binomial com p :0,5en :3 . Admita que XeY são independentes.Determine P X = 0 Y = 2 . Obtenha a função de probabilidade conjunta do X e Y e do produto XY.Calc
A função de probabilidade conjunta entre as variáveis aleatórias X e Y é apresentada na próxima tabela.Obtenha as tabelas marginais de frequência.X e Y são independentes?Calcule a covariância e a corr