Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 6.Exercícios - Ex. 72

Construa um gráfico de probabilidade normal dos dados de concentração de sólidos suspensos do exercício 6.24. Parece razoável supor que a concentração de sólidos suspensos na água proveniente de um determinado lago seja normalmente distribuída?

Passo 1

Os dados de concentração de sólidos suspensos estão no eixo horizontal e o padrão dos valores normais estão no eixo vertical.

Se os dados contiverem n valores de dados, então os valores normais padronizadas são os valores na tabela III correspondente a uma área de (ou a área mais próxima) com

O menor valor padronizado corresponde ao menor valor de dados, o segundo menor valor padronizado corresponde ao segundo menor valor de dados e assim por diante.

Passo 2

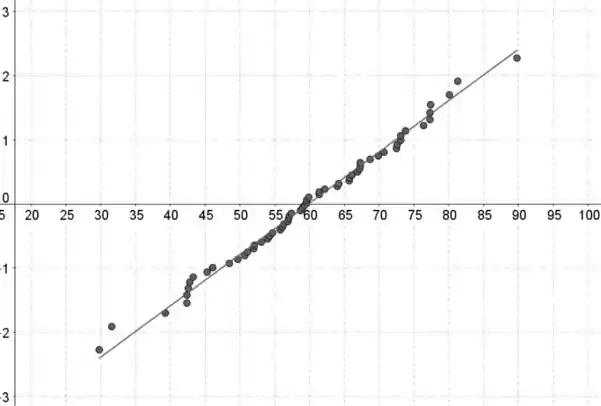
Parece razoável presumir que os dados são normalmente distribuídos, porque o padrão no gráfico de probabilidade normal é quase linear.

Resposta

Parece razoável presumir que os dados são normalmente distribuídos, porque o padrão no gráfico de probabilidade normal é quase linear.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O número de respostas incorretas num teste de verdadeiro ou falso, para uma amostra aleatória de 15 estudantes, foi registrado como se segue: 2, 1, 3, 0, 1, 3, 6, 0, 3, 3, 5, 2, 1, 4 e 2. Determine(a)

Em relação aos tempos que dez pacientes esperaram no consultório médico antes de receber tratamento, no Exercício 8.4, determine(a) a amplitude;(b) o desvio-padrão.

Uma amostra aleatória de empregados de uma indústria local prometeu as seguintes doações, em dólares, para uma gestão de fundos: 100, 40, 75, 15, 20, 100, 75, 50, 30, 10, 55, 75, 25, 50, 90, 80, 15, 2

Determine a probabilidade de que uma amostra aleatória de 25 observações, de uma população normal com variância σ 2 = 6 , terá uma variância amostrai s 2 (a) maior que 9,1;(b) entre 3,462 e 10,745. As

A variável aleatória X , que representa o número de cerejas em um bolinho, tem a seguinte distribuição de probabilidade:(a) Determine a média μ e a variância σ 2 de X (b) Determine a média μ X - e a v