Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 8.Exercícios - Ex. 23
A variável aleatória , que representa o número de cerejas em um bolinho, tem a seguinte distribuição de probabilidade:
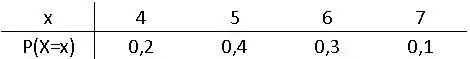
(a) Determine a média e a variância de
(b) Determine a média e a variância da média para amostras aleatórias de 36 bolinhos de cereja.
(c) Determine a probabilidade de que o número médio de cerejas em 36 bolinhos seja menor que 5,5.
Passo 1
Falaa, meu querido/minha querida. Relembrando as fórmulas já conhecidas por nós:
A média nós encontramos multiplicando cada valor de por sua probabilidade de ocorrer.
Já a variância, é dada pelo diminuído pela média, ao quadrado, e multiplicado pela sua probabilidade de ocorrência:
Então, bora para os cálculos!!!
Passo 2
Encontrando a média solicitada pelo enunciado e usando a fórmula do Passo 1:
Já a variância é dada por:
Passo 3
O espaço amostral é dado por . Usando esse fato e os resultados da letra (a), nós temos a média:
Já a variância da média é:
Passo 4
Para encontrarmos a probabilidade aleatória solicitada, vamos usar a fórmula a seguir:
Sendo assim, a probabilidade é:
Usando a tabela de valores de distribuição normal, encontramos:
Resposta
a) ,
b) ,
c)