Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 7.Problemas - Ex. 30

Suponha que a variável aleatória bidimensional (X,Y) seja uniformemente distribuída sobre o triângulo da Fig. 7.16.

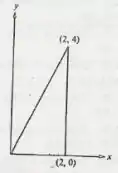
Estabeleça a fdp marginal de X e a de Y, e calcule V X e   V Y .

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos a nossa variância. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser relembrar o que o exercício nos deu. Preparado??

l 1 → y = 2 x

f x , y = 1 4 ,   0 < x < 2   ,     0 < y < 2 x y 2 < x < 2 ,     0 < y < 4

Com essa estrutura de probabilidade, podemos arrumar para botar em função do primeiro valor da distribuição dela. Lembra como faz?? Não?? Vai lá na teoria que eu te esperoaqui...

Achou?? Então me diz aii...

E X = ∑ x p ( x )

E X = ∫ x   f x d x

V X = E X 2 - E X 2

Com isso, podemos começar as nossas contas.

g x = 1 4 ∫ d y = x 2

h y = 1 4 ∫ d x = 1 8 4 - y  

Passo 3

Pronto!! Agora é só obter nossa esperança!!

V X = E X 2 - E 2 X

V X = 2 9  

V Y = E Y 2 - E 2 Y

V Y = 8 9

Resposta

V X = 2 9  

V Y = 8 9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a média da v.a. X do Problema 4.
A v.a. contínua X tem f.d.pf (x) = {[[3 x^2 , - 1 = x = 0],[0 , c a s o c o n t r á r i o]]) á (b) Calcule E ( X ) e V a r ( X ) .
A v.a. contínua X tem f.d.p f x = 3 x 2 , - 1 ≤ x ≤ 0 0 , c a s oc o n t r á r i o á (a) Se b for um número que satisfaz –1 , calcule P(Xb| X .
Determine a esperança e a variância da v.a. cuja f.d.p. é f x = s e nx , 0 ≤ x ≤ π 2 0 , c a s oc o n t r á r i o . á
Dada a v.a.determine a média e a variância de Z, sabendo-se que a f.d.p. de X é