Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 2.Problemas - Ex. 4

Contou-se o número de erros de impressão da primeira página de um jornal durante 50 dias, obtendo-se os resultados abaixo:

Represente os dados graficamente.

Faça um histograma e um ramo-e-folhas.

Passo 1

Fala ai meus queridos, para resolver esse problema, primeiro vamos pegar cada um desses números que aparecem no nosso enunciado e vamos plotá-los usando uma ferramenta gráfica. Podemos fazer um gráfico simples de barras, com uma barra para cada dado e ficamos com:

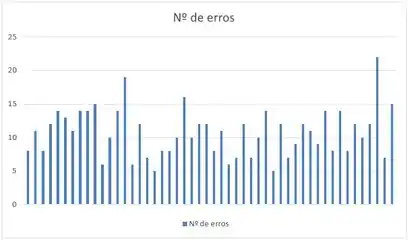
Então aqui temos um histograma que nos mostra como como foram distribuídos o número de erros em cada um dos 50 dias, o que nos permite observar como estão distribuídos os erros durante esse período.

Passo 2

Belezinha, agora com os mesmos dados dividimos os valores nas seguintes faixas:

E contamos o número de aparições de cada números podemos montar o seguinte histograma:

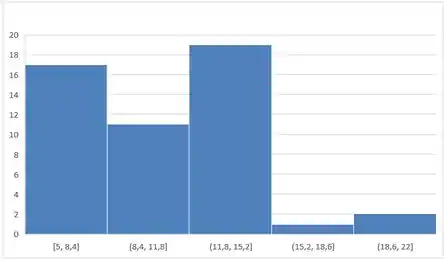
Agora montamos um histograma um pouco diferente. Nossas faixas representam números de erros no Jornal, então podemos perceber que existe uma maior incidência de baixos números de erros, em comparação com um maior número de erros.

Passo 3

Por fim, o gráfico ramo e folhas fica, onde montamos 3 ramos, para 9 folhas:

Os gráficos de ramo-e-folha costumam ser mais livres e acabam gerando diversas interpretações. No caso podemos ver que as folhas dos ramos 0 e 1 estão mais cheias que as folhas do ramo 2, e podemos concluir algo semelhante ao que concluímos no Passo 2. Temos que são baixas as frequentes aparições de erros no Jornal e são raros os casos que vemos muitos erros nesse Jornal.

Resposta

Gráficos e imagens.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Distribuição Beta. Uma v.a. X tem distribuição beta com parâmetros α0 ,β0 , se sua f.d.p. for dada por: f x = 1 B ( α ,β ) × x α - 1 × 1 - x β - 1 ,0x1 0 ,c a s oc o n t r á r i o á Aqui, B ( α ,β ) é

Para uma v.a. com distribuição qui-quadrado, com ν graus de liberdade e ν par, vale a seguinte fórmula: P χ 2 vc = e - c / 2 × ∑ j = 0 v 2 - 1 c 2 j j ! Calcule essa probabilidade para os seguintes ca

Se na distribuição t de Student colocarmos ν=1 , obteremos a distribuição de Cauchy, fx = 1 π × 1 1 + x 2 . Mostre que E ( X ) não existe.

Resolva a mesma questão para uma v.a. Y ~ χ 2( 5 ) .

Distribuição de Weibull. Um modelo que tem muitas aplicações na teoria da confiabilidade é o modelo de Weibull, cuja f.d.p. é dada por: f x = ∝ β x β - 1 e - α x β ,x ≥ 0 0 ,x0 , Onde α eβ são constan