Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 6º - Capítulo 7.Problemas - Ex. 52

Distribuição Beta. Uma v.a. X tem distribuição beta com parâmetros α > 0 ,   β > 0 , se sua f.d.p. for dada por:

f x = 1 B ( α ,   β ) × x α - 1 × 1 - x β - 1 ,   0 < x < 1 0 ,                                                                                                           c a s o   c o n t r á r i o

Aqui, B ( α ,   β ) é a função beta, definida por:

B α ,   β = ∫ 0 1 x α - 1 × 1 - x β - 1 d x .

É possível provar que B ( α ,   β )   =   Γ ( α ) Γ ( β )   /   Γ ( α   +   β ) . A figura abaixo mostra a densidade da distribuição beta para α   =   β   =   2 .   Para esse caso, calcule P ( X ≤   0,2 ) . Calcule a média e a variância de X   para α   =   β   =   2 .

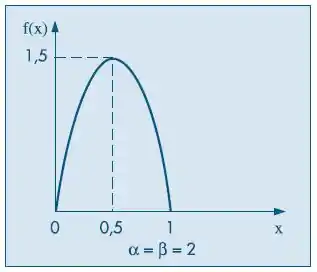
Passo 1

A Distribuição Beta possui f.d.p. no intervalo 0 < x < 1 , dada por:

f x = 1 B ( α , β ) × x α - 1 × 1 - x β - 1 = Γ α + β Γ α × Γ β × x α - 1 × 1 - x β - 1

Para α = β = 2 , temos:

f x = Γ 4 Γ 2 × Γ 2 × x × 1 - x = 6 × x × 1 - x .

Resposta

Assim,

P X ≤ 0,2 = 6 × ∫ 0 0,2 x × 1 - x d x = 6 × x 2 2 - x 3 3 0 0,2 = 0,104 ;

E X = 6 × ∫ 0 1 x 2 × 1 - x d x = 6 × x 3 3 - x 4 4 0 1 = 0,5 ;

E X 2 = 6 × ∫ 0 1 x 3 × 1 - x d x = 6 × x 4 4 - x 5 5 0 1 = 0,3

V a r X = E X 2 - E X 2 = 0,05 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Eventos incomuns. No Exercício 20, seria incomum para um funcionário trabalhar duas horas extras? Explique seu raciocínio.
Encontrando probabilidades. Use a distribuição de probabilidades que você construiu no Exercício 20 para encontrar a probabilidade de selecionar aleatoriamente um funcionário que tenha feito.(a) duas
Construindo e representando graficamente distribuições discretas de probabilidade. Nos exercícios 19 e 20, (a) construa uma distribuição de probabilidade e (b) faça um gráfico da distribuição de proba
Encontrando probabilidades. Use a distribuição de probabilidades que você construiu no Exercício 20 para encontrar a probabilidade de selecionar aleatoriamente um funcionário que tenha feito.(c) entre
Encontrando o valor esperado Nos exercícios 37 e 38, encontre o ganho líquido esperado do jogador para uma rodada do jogo. Se x é o ganho líquido de um jogador em um jogo de azar, então E(x) é usualme