A corrente (em necessária para produzir um determinado nível de brilho em um tubo de televisão foi medida para dois tipos diferentes de vidro e três diferentes tipos de fósforo, gerando os dados a seguir ("Fundamentals of Analysis of Variance", Industrial Quality Control, 1956, p. 5-8).

Supondo que ambos os fatores sejam fixos, teste versus no nível 0,01. Em seguida, se não puder ser rejeitada, teste os dois conjuntos de hipóteses de efeito principal.

E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

Supondo que ambos os fatores sejam fixos, teste versus no nível 0,01. Em seguida, se não puder ser rejeitada, teste os dois conjuntos de hipóteses de efeito principal.

,, que rende o

que acompanha a tabela ANOVA.

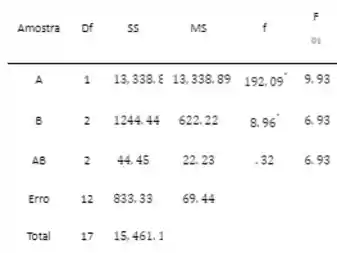
Claramente, é insignificante, então não é rejeitado. Ambos e são rejeitados, pois ambos são maiores que os respectivos valores críticos. Tanto o tipo de fósforo quanto o tipo de vidro afetam significativamente a corrente necessária para produzir o nível de brilho desejado.