Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.2 - Ex. 6
Um criador tem constatado uma proporção de do rebanho com verminose. O veterinário alterou a dieta dos animais e acredita que a doença diminuiu de intensidade. Um exame em do rebanho, escolhidas ao acaso, indicou 8 delas com verminose. Ao nível de , há indícios de que a proporção diminuiu??
Passo 1
Vamos lá, primeiro de tudo definir nossa variável:
Supondo que a população seja normalmente distribuída, podemos utilizar a seguinte aproximação:
Do enunciado vimos que
Passo 2
Agora vamos definir nossa estratégia de teste:
Lembrando sempre que a hipótese nula é quem carrega o sinal de igual .
Repare que se rejeitamos temos evidencias de que realmente houve uma diminuição na proporção de doentes; agora caso aceitamos a hipótese nula, temos motivos para acreditar que essa proporção se manteve pelo menos igual a constatação do criador.
Em ambos os casos vamos obter uma resposta coerente com a questão em jogo (repare que se invertermos os sinais, não vamos obter respostas dignas)
Se considerarmos um nível de , teremos a seguinte região crítica:
Como neste caso a hipótese alternativa carrega o sinal de menos, tomaremos uma RC unilateral inferior.
E então:
Olhando na tabela de distribuição normal:
Portanto:
Passo 3
Buscando esse valor na tabela:
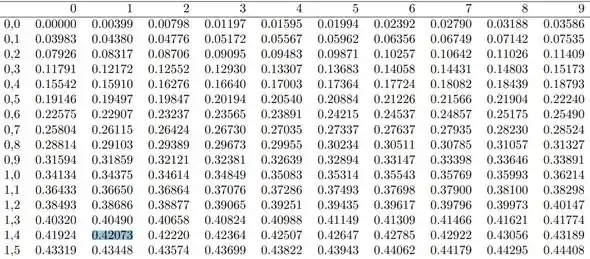
Para
No final das contas, a RC fica assim:
Realizando o teste sob a hipótese nula:
Resposta
Portanto não pertence à RC, devemos então aceitar e concluir que NÃO existem evidencias de que, a nova dieta passada pelo veterinário, realmente diminuiu a proporção da doença no rebanho.