Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 2.Exercícios - Ex. 11
Os currículos de dois candidatos do sexo masculino para a vaga de professor universitário de química são colocados no mesmo arquivo dos currículos de duas candidatas do sexo feminino. Surgem duas vagas e a primeira, para professor-assistente, é preenchida selecionando-se um dos quatro candidatos aleatoriamente. A segunda vaga, para instrutor, é então preenchida selecionando-se aleatoriamente um dos três candidatos remanescentes. Usando a notação M2FX, por exemplo, para denotar o evento simples no qual a primeira vaga é preenchida pelo segundo candidato do sexo masculino e a segunda vaga é preenchida pela primeira candidata do sexo feminino:
(a) Liste os elementos do espaço amostral .
(b) Liste os elementos de S que correspondem ao evento em que a posição de professor-assistente é preenchida por um candidato do sexo masculino.
(c) Liste os elementos de S que correspondem ao evento em que exatamente uma das duas posições é preenchida por um candidato do sexo masculino.
(d) Liste os elementos de S correspondentes ao evento em que nenhuma das posições é preenchida por um candidato do sexo masculino.
(e) Liste os eventos de S correspondentes ao evento .
(f) Liste os eventos de S correspondentes ao evento .
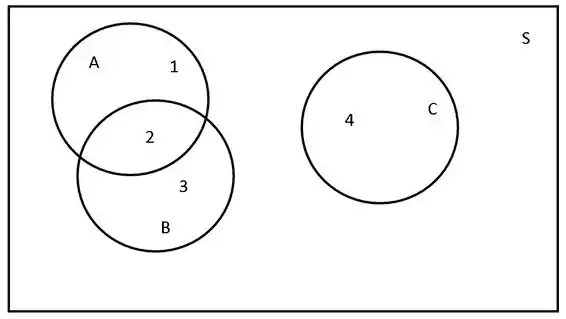
(g) Construa um diagrama de Venn para ilustrar as intersecções e uniões dos eventos A, B e C.
Passo 1
Falaa, meu querido/minha querida. Vamos denotar como , , e , as letras são para masculino e para feminino, onde as posições são importantes para o experimento, por primeira representar professor-assistente e a segunda instrutora. Então, bora lá encontrar o espaço amostral e os eventos que o enunciado nos pede!!!
Passo 2
Para o espaço amostral devemos incluir todas as possibilidades. Então, temos:
Passo 3
O evento, onde o professor-assistente é do sexo masculino, a primeira posição deve ser preenchida pro . Logo:
Passo 4
Para que exatamente uma das posições seja preenchida por uma pessoa do sexo masculino, o evento é:
Passo 5
Caso nenhuma seja preenchida por uma pessoa do sexo masculino, todas as posições contém , então:
Passo 6
A intersecção de dois eventos é onde ocorre de forma simultânea nos dois eventos. Sendo assim:
Passo 7
Quase terminando!! A união de dois eventos, são todos os acontecimentos dos dois eventos.
Passo 8
O diagrama do espaço amostral e dos eventos é representado abaixo:
Resposta
Resolução nos passos anteriores.