Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Probabilidade, um curso moderno com aplicações, de Sheldon Ross- Ed: 8º - Capítulo 4.Problemas - Ex. 8

Se o dado do problema 4.7 é honesto, calcule as probabilidades associadas às variáveis aleatórias nas letras (a) e (d).

Passo 1

Bom, na letra (a) do problema 4.7, descobrimos que os casos que temos para calcular são:

X = 1 ,   2 ,   3 ,   4 ,   5 ,   6

Cada X representa ao máximo valor que pode ocorrer no lançamento de dois dados, vamos ver nossa tabelinha novamente:

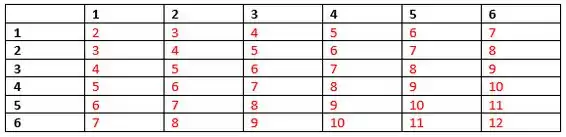
façamos então:

P X = 1 = 1 36 ;                                       P X = 2 = 3 36 ;                                                 P X = 3 = 5 36

P X = 4 = 7 36 ;                                       P X = 5 = 9 36 ;                                           P X = 6 = 11 36

Passo 2

Vamos ver agora, o que ocorre na situação descrita no item (d). já sabemos do problema anterior que as variáveis aleatórias são:

X = - 5 ,   - 4 ,   - 3 ,   - 2 ,   - 1 ,   0 ,   1 ,   2 ,   3 ,   4 ,   5

olhando para a tabela novamente, vai ficar fácil:

P X = - 5 = P X = 5 = 1 36 ; P X = - 4 = P X = 4 = 2 36 ; P X = - 3 = P X = 3 = 3 36

P X = - 2 = P X = 2 = 4 36 ;   P X = - 1 = P X = 1 = 5 36 ;   P X = 0 = 6 36

Matamos mais uma, uhuuuulll. lolololololol

Resposta

Ver resolução.

Exercícios de Livros Relacionados

No Problema 4.15, chame de time 1 o time com a pior campanha, time 2 aquele com a segunda pior campanha, e assim por diante. Suponha que Y , represente o time que tenha ai-ésima chance de escolher um
a) Um inteiro N é selecionado aleatoriamente de { 1,2 , … , 10 3 } , onde cada um dos números tem a mesma probabilidade de ser selecionado. Qual é a probabilidade de que N seja divisível por 3? por 5?
A loteria de novatos da Associação Nacional de Basquete (NBA) envolve os 11 times que tiveram a pior campanha durante o ano. Um total de 66 bolas é colocado em uma urna. Cada uma dessas bolas tem esta
Suponha que a função distribuição de X seja dada por: 0 b0 b 40≤ b1 1 2 + b - 1 4 1 ≤ b2 11 122 ≤ b3 13 ≤ b (a) Determine P{X = i}, i = 1,2,3.(b) Determine P{ 1 2x 3 2 }.
O valor esperado da distribuição de probabilidade de uma variável aleatória é sempre um dos valores possíveis de x? Explique.