Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios Suplementares - Ex. 70

Os dados resumidos a seguir sobre a resistência a dobramentos (lb-in/in) das juntas foram extraídos do artigo "Bending Strength of Corner Joints Constructed with Injection Molded Splines" (Forest Products J., Abril, 1997, p. 89-92).

a. Calcule um limite de confiança inferior a 95% para a resistência média real das juntas com revestimento lateral. b. Calcule um limite de previsão inferior de 95% para a resistência de uma única junta com revestimento lateral. c. Calcule um intervalo que, com confiança de 95%, inclua os valores de resistência para pelo menos 95% da população de todas as juntas com revestimentos laterais. d. Calcule um intervalo de confiança de 95% para a diferença entre as resistências médias reais dos dois tipos de juntas.

Passo 1

  1. Determine o valor t olhando na linha começando com graus de liberdade d f = n - 1 = 10 - 1 = 9 e na coluna com α   = 1 - c = 0 . 05 na tabela da distribuição T de Student:

    2. t α = 1.83

    A margem de erro é:

    E = t α 2 ∙ s n = 1.833 ∙ 5.96 10   ≈ 3.454

    Os limites do intervalo de confiança tornam-se então:

    x - - E = 63.23 - 3.4547 = 59.7753

    Assim, o limite de confiança 95% inferior é 59 . 7753 .

    Passo 2

  2. Determine o valor t olhando na linha começando com graus de liberdade d f = n - 1 = 10 - 1 = 9 e na coluna com α   = 1 - c = 0.05 na tabela da distribuição T de Student:

    3. t α = 1.83

    A margem de erro é:

    Os limites do intervalo de confiança tornam-se então:

    x - - E = 63.23 - 11.459 = 5 1 . 77 21

    Assim, o limite de confiança 95% inferior é 5 1 . 77 21 .

    Passo 3

  3. Determine o valor t olhando na linha começando com graus de liberdade d f = n - 1 = 10 - 1 = 9 e na coluna com α   = 1 - c 2 = 0 . 0 2 5 na tabela da distribuição T de Student:

    4. t α = 2.262

    A margem de erro é:

    E = t α 2 ∙ s n = 2.262 ∙ 5.96 10   ≈ 4.2632

    Os limites do intervalo de confiança tornam-se então:

    x - - E = 80.95 - 4.2632 = 76.6868

    x - + E = 80.95 + 4.2632 = 85.2132

    Assim, o limite de confiança 95% inferior é 59 . 7753 .

  4. Determine os graus de liberdade (arredondados para o inteiro mais próximo):

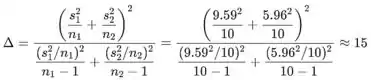
Determine o valor t olhando na linha começando com graus de liberdade df=15 e na coluna com α = 1 - c / 2 = 0 . 025 na tabela de distribuição t de Student no apêndice:

t α 2 = 2.131

A margem de erro é então:

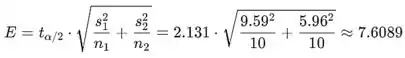
Os pontos finais do intervalo de confiança para μ 1 - μ 2 são:

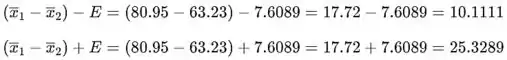
Resposta

  1. 59.7753
  2. 51.7721
  3. 76.6868,85.2132
  4. ( 10.1111,25.3289 )

Exercícios de Livros Relacionados

Um engenheiro mecânico quer comparar as propriedades de resistência de vigas de aço com as de vigas semelhantes feitas com uma liga específica. O mesmo número de vigas, n , de cada tipo será testado.
A tabela a seguir fornece dados resumidos sobre a resistência à compressão ao cubo N / m m 2 de espécimes de concreto feitos com uma mistura pulverizada de combustível pulverizada ("A Study of Twenty-
Um artigo do Consumer Reports de novembro de 1983 comparou vários tipos de pilhas. A vida útil média das pilhas alcalinas AA Duracell e das pilhas alcalinas AA Eveready Energizer foi dada como 4,1 hor
Sejam μ 1 e μ 2 As densidades médias reais de dois tipos diferentes de tijolo. Assumindo a normalidade das duas distribuições de densidade, teste H 0 : μ 1 - μ 2 = - 10 versus H a : μ 1 - μ 2 ≠ 0 , us
O artigo "Evaluation of a Ventilation Strategy to Prevent Barotrauma in Patients at High Risk for Acute Respiratory Distress Syndrome" (New Engl. J. of Med., 1998, p. 355 - 358 ) relatou um experiment