Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 31
Os dados a seguir foram obtidos de um estudo sobre determinado método de preparar álcool puro proveniente da corrente das refinarias (“Direct Hydration of Olefins”, industrial and Eng. Chemistry, 1961, p. 209–211). A variável independente x é a velocidade espacial horária do volume e a variável dependente y é a quantidade de conversão de isobutileno.
Passo 1
- Usando o Minitab, a equação de regressão é y = 13,6 + 11,4x - 1,72x2.
- Novamente, usando o Minitab, os valores previstos e residuais são:
- Da saída do Minitab, s²=MSE = 2.040 e R²= 94.7%. O modelo quadrático assim explica 94,7% da variação nos y’s observados, o que sugere que o modelo se ajusta os dados muito bem.
- sugere que podemos estimar por e, em seguida, tire a raiz quadrada para obter o desvio padrão estimado de cada
- é estimado por , então . Com e , o P.I desejado é
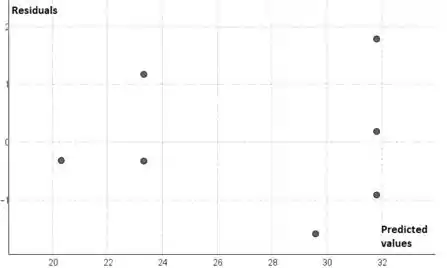
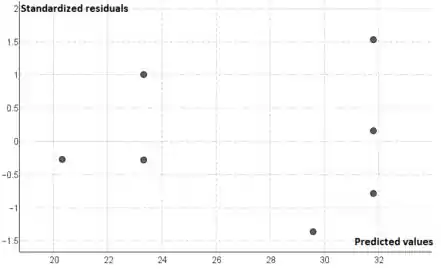
O gráfico residual é consistente com um modelo quadrático (nenhum padrão que sugira modificação), mas fica claro pelo gráfico de dispersão que o ponto (6, 20) teve uma grande influência no ajuste – é o ponto que forçou a quadrática ajustada a ter um máximo entre 3 e 4 em vez de, por exemplo, continuar a curvar-se lentamente para cima até um máximo em algum lugar à direita de x = 6
Passo 2
residual. Isto dá , (e da mesma forma para todos os pontos) 10,59,1.236, 1.196, 1.196, 1.196 e .233 como os desvios padrão estimados dos resíduos. O os resíduos padronizados são então calculados como , (e similarmente) 1,10, -1,28, -0,76, 0,16, 1,49 e -1,28, nenhum dos quais é incomumente grande. (Observação: regressão do Minitab saída pode produzir esses valores.) O gráfico residual resultante é praticamente idêntico ao gráfico de b , então padronizar usando apenas s não seria produzir os resíduos padronizados corretos.
Passo 3
Resposta
Ver o desenvolvimento