Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 11.Exercícios - Ex. 23

Os dados a seguir foram obtidos em um experimento realizado para investigar se a resistência à compressão de cilindros de concreto depende do tipo de material de revestimento usado ou da variabilidade em lotes diferentes ("The Effect of Type of Capping Material on the Compressive Strength of Concrete Cylinders", Proceedings ASTM, 1958, p. 1166-1186). Cada um dos números é um total da célula x i j tendo por base K = 3 observações.

Além disso, ∑ ∑ ∑ x i j k 2 = 16.815.853 e ∑ ∑ x i j 2 = 50.443.409. Obtenha a tabela ANOVA e, em seguida, teste as hipóteses H 0 G versus H a G , H 0 A versus H a A e H 0 B versus H a β , no nível 0,01 , supondo que o revestimento seja um efeito fixo e os lotes, um efeito aleatório.

Passo 1

E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

As quantidades resumidas incluem

x 1 ∙ ∙ = 9410 , x 2 ∙ ∙ = 8835 , x 3 ∙ ∙ = 9234 , x ∙ 1 = 5432 , x ∙ 2 ∙ = 5684 , x ∙ 3 ∙ = 5619 , x ∙ ι ∙ = 5567 , x ∙ 3 ∙ = 5177 , x ∙ ω = 27,479 , C F = 16,779,898.69 , Σ x i ∙ ∙ 2 = 251,872,08 1 , Σ x ∙ j ∙ 2 = 151,180,459 , resultando na tabela ANOVA que acompanha.

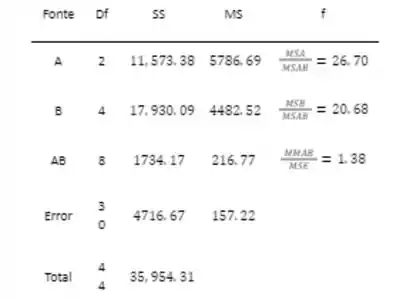
Como 1.38 < F . 01,8 , 30 = 3.17 , H o G não pode ser rejeitado e continuamos: 26.70 ≥ F 01,2 , 8 = 8.65 , and 20.68 ≥ F . 01,4 , 8 = 7.01 , então ambos H o A e H o B são rejeitados. Tanto o material de cobertura quanto os diferentes lotes afetam a resistência à compressão dos cilindros de concreto.

Resposta

Tanto o material de cobertura quanto os diferentes lotes afetam a resistência à compressão dos cilindros de concreto.

Espero que tenham aprendido com essa questão, até a próxima !

Exercícios de Livros Relacionados

11-95. Suponha que estejamos ajustando uma linha e desejamos teruma variância do coeficiente de regressão , tão pequena quantopossível. Onde as obscrvações x,. i = 1. 2. ..., n, devem ser obtidaspara
11-94.Suponha que tenhamos considerado o modelo de regressãode linha reta Y = β a + β 1 x 1 + ϵ porém a resposta é afetada por uma segunda variável x,, tal que afuncão verdadeira de regressão seja E Y
11-97. Considere uma situação em que ambas as variáveis Y e Xsejam aleatórias. Faça s, e s, serem os desvios-padráo amostrais dosvalores observados de x's e y's. respectivamente. Mostre que umaexpress
11-96. Minimos Quadrados Ponderados. Suponha que estejamosajustando a linha a variância porém. de Y depen-de do nível de x; ou seja. V Y i ∣ x i = σ i 2 = σ 2 w i i = 1,2 , … , n sendo as constantes w
11-98. Suponha que estejamos interessados em ajustar um modelode regressão linear simples em que a interseção, n,seja conhecida.a) Encontre o estimador de mínimos quadrados para b) Qual é a variância