Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios Suplementares - Ex. 72
Os dados a seguir foram reproduzidos de um gráfico de dispersão apresentado no artigo “Urban Emissions Measured with Aircraft” (J. of the Air and Waste Mgmt. Assoc., 1998, p. 16–25). A variável de resposta é NOy e a variável explicativa é CO.
a. Ajuste um modelo apropriado aos dados e avalie a sua utilidade. b. Preveja o valor de NOy que resultaria de uma observação a mais quando CO for 400. Faça os cálculos de maneira que transmita informações sobre precisão e confiabilidade. Será que NOy pode ser previsto com precisão? Explique. c. O maior valor de CO é bem maior que os outros valores. Essa observação parece ter tido um impacto significativo sobre a equação ajustada?
Passo 1
- Dos graus de liberdade, , e o fato de que
- A linha de regressão, da saída do SAS, é
- O coeficiente de determinação pode dizer se existe uma relação linear útil entre as duas variáveis.
- O coeficiente de correlação da amostra r é dado por
- Os dados não são fornecidos; então veja o valor de y quando
o tamanho da amostra n é
Assim, a estimativa pontual quando , é
Passo 2
O coeficiente de determinação, , é
Os valores de SSE e SST são fornecidos na saída do SAS; assim, o coeficiente de determinação é
O coeficiente de determinação é grande (próximo de 1); assim, parece que existe uma relação linear útil entre as variáveis dadas
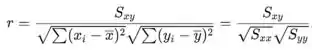
O valor do coeficiente de correlação da amostra é
Isso ocorre porque o coeficiente de correlação da amostra é a raiz quadrada do coeficiente de determinação.
Passo 3
o, quando o nível de salinidade é 40, o valor do nível de nitrato -9,18-9,18 que não pode ser verdadeiro porque não pode ser negativo. Por isso, não use.
Resposta
- 28.635
- R²=0.92
- R=0.96
- Não usar