Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 5c
Os dados a seguir referem-se a uma amostra de 5 alunos que informaram, no início do curso, seu peso e idade.
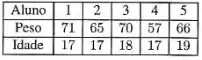
- Encontre a média e o desvio padrão do peso dos alunos com 17 anos.
- Construa o diagrama de Peso por Idade.
- Obtenha o coeficiente de correlação entre peso e idade.
Passo 1
- Para calcular o coeficiente de correlação vamos ter que encontrar a Covariância dessas variáveis e para isso teremos que descobrir a média dessas variáveis. Além disso vamos ter que calcular a variância dessas variáveis e então utilizar a fórmula:
Passo 2
Na Seção 2 desse capítulo você encontra, nas questões 4 e 6, o passo a passo para chegar nos seguintes valores:
Passo 3
Calculando a correlação
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere X e Y vida útil, em anos, de dois componentes em um sistema eletrônico. Se a função de densidade conjunta dessas variáveis é f x , y = e - ( x + y ) , x0 , y0 0 ,c a s oc o n t r á r i o á D
Se a distribuição de probabilidade conjunta de X e Y é dada por f x , y = x + y 30 ,x = 0 ,1 ,2 ,3 ; y = 0 ,1 ,2 , Determine(a) P ( X ≤ 2 ,Y = 1 ) ;(b) P ( X2 ,Y ≤ 1 ) ;(c) P ( XY ) ;(d) P X + Y = 4 .
Considere um experimento que consiste em duas jogadas de um dado balanceado. Se X é o número de resultados quatro e Y é o número de resultados cinco obtidos em duas jogadas do dado, determine(a) a dis
Suponha que X e Y tenham a seguinte distribuição de probabilidade conjunta:(a) Determine a distribuição marginal de X.(b) Determine a distribuição marginal de Y.
Determine os valores de c de modo que as seguintes funções representem as distribuições de probabilidade conjuntas das variáveis aleatórias X e Y:(a) f x ,y = c x y , para x = 1 ,2 ,3 ; y = 1 ,2 ,3 ;(