Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 10.Exercícios - Ex. 14
Use o procedimento de Tukey nos dados do Exercício 4 para identificar diferenças no tempo de voo médio real entre os quatro tipos de mosquito.
Passo 1
O Método T para Identificar μ Significativamente Diferente
Encontre o valor na Tabela A.10. no apêndice do livro para dado α. Calcule e e liste as médias amostrais em ordem crescente. Calcular
e sublinhe os pares das médias da amostra que diferem em menos de ww. O par de amostras que não são sublinhados pela mesma linha correspondente à população ou tratamento significa que são significativamente diferentes.
Da tabela mencionada, e ,
onde esse valor foi estimado usando a tabela (você também pode calcular ou pesquisar no Google). O valor de MSEMSE é dado no exemplo
Calcule o valor w como
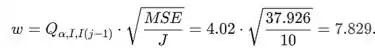
Primeira ordene a amostra significa
A tabela a seguir resume as diferenças para que você não precise seguir explicações se souber como computá-las
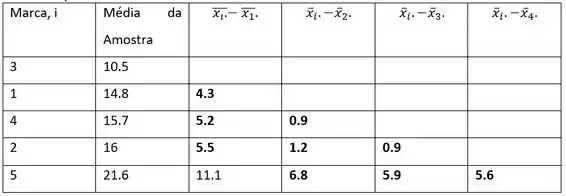
onde os valores em negrito são menores que w.
Passo 2
analiticamente, comece com a média da primeira e da segunda amostra e continue assim até que todos os pares sejam calculados (depois análise)
que indica que o par (1,2) deve ser sublinhado como um par:
Faça o mesmo para todos os pares
então o par (1,3) não deve ser sublinhado como um par;
O próximo par é (1,4)
então o par (1,3) não deve ser sublinhado como um par;
Para o par (1,5)
então o par (1,5) não deve ser sublinhado como um par.
Vá para os próximos pares, começando com (2,3) até você chega até (2,5) que conclui todos os pares
Passo 3
então o par (2,3) deve ser sublinhado como um par;
O próximo par é (2,4)
então o par (2,4) deve ser sublinhado como um par;
O próximo par é (2,5)
então o par (2,5) deve ser sublinhado como um par;
O próximo par é (3,5)
o par (3,5) deve ser sublinhado como um par;
O próximo par é (4,5)
o par (4,5) deve ser sublinhado como um par;
As conexões podem ser representadas como
A conclusão é que não há diferenças significativas entre pares que estão conectados por uma linha; e há uma diferença significativa entre o par (1,5), que não está conectado
Resposta
