Deseja-se comparar a durabilidade de amortecedores fabricados pelas empresas A e B. A medida observada é o índice de resistência de cada peça testada em laboratório, que é assumido ter a mesma variabilidade nas duas empresas. Os resultados obtidos são apresentados a seguir.
![]()
Fazendo as suposições necessárias, qual a conclusão ao nível 2%?
Passo 1
Fala ai meu querido, temos que comparar duas médias nesse exercício, de duas empresas que tem a mesma variância, então estamos lidando com o Caso 3A da seção 9.2.
Passo 2
Vou utilizar uma planilha do Excel para garantir contas corretas e para facilitar nossa vida. Vou utilizar uma ferramenta de “Análise de Dados” com a opção “Teste-t: duas amostras presumindo variâncias equivalentes”, que nos dá os seguintes resultados:
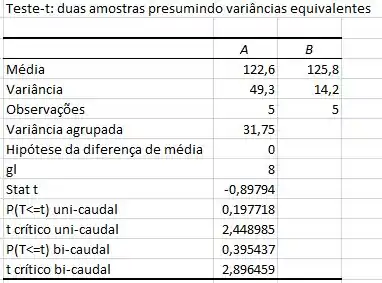
Passo 3
Como nosso teste de hipótese é:
Temos um teste bi-caudal e precisamos calcular nosso :
Sendo a variância agrupada:
Calculando esses valores, você irá encontrar:
Que é o valor que o Excel chama de Stat t.
Passo 4
Com , temos que nossa região crítica é , portanto nosso está dentro da área de aceitação, e podemos afirmar que não existe diferença entre a durabilidade dos amortecedores das empresas A e B.
Resposta
Ei, a resposta está no passo a passo :)