Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 6
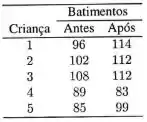
Para estudar o impacto de cenas violentas em desenhos animados, 5 crianças tiveram seus batimentos cardíacos medidos, antes e após assistirem a um desenho comercialmente veiculado por uma grande emissora de TV. Os dados são apresentados a seguir:
Qual a conclusão, considerando-se um nível de significância Que suposições são necessárias?
Passo 1
E ai meu querido, para resolver essa questão temos que fazer um teste de hipótese para testar se houve mudança significativa nos batimentos cardíacos das crianças após as cenas violentas nesse problema:
Vamos seguir o passo a passo do Caso 1 descrito na seção 9.2 do livro. Recomendo que observe a resolução do Exemplo 9.3 porque é similar. Esse exercício também é semelhante com o exercício 1 dessa seção.
Passo 2
Utilizarei uma ferramenta de “Análise de Dados” do Excel, chamada de “Teste-T: duas amostras em par para médias” que vai nos dar o seguinte resultado:
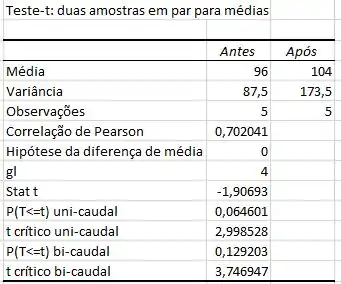
Passo 3
Vamos utilizar a distribuição de t-Student nesse problema e podemos calcular através da seguinte fórmula:
Após esses cálculos o valor encontrado para que é o que o Excel chama de Stat t.
Passo 4
Como estamos tratando de um teste bilateral, temos que nossa região crítica será . Como ele se encontra na região de aceitação e podemos concluir que não existe diferença significativa entre as médias dos batimentos cardíacos das crianças.
Resposta
Ei, a resposta está no passo a passo :)