Determinar os pontos da distribuição qui-quadrado de modo que a área subtendida entre eles seja igual a 0,95, sendo , admitindo-se que as áreas laterais a esses pontos sejam iguais.

Oi pessoal. Vamos pensar juntos neste exercício?! Iremos iniciar relembrando de algumas teorias.

A distribuição Qui-Quadrado () constitui-se de uma família de curvas, cada qual caracterizada pelos graus de liberdade e ela está tabelada em função do parâmetro . O tipo mais frequente é a tabela unicaudal à direita:

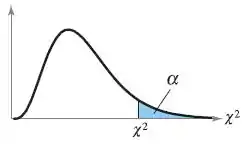
Para uma dada probabilidade e para um dado , o corpo da tabela fornece o valor de tal que , probabilidade essa representada, na figura, pela região hachurada.

Lembrando que a distribuição tem as seguintes diferenças, em relação à normal:

• é sempre positiva;
• é assimétrica;
• a tabela fornece o valor do a partir de uma probabilidade e um certo número de graus de liberdade .

Então vamos lá para o nosso exercício. Do nosso enunciado, temos que:

• ;
• .

Como queremos o teste bilateral:

Pela tabela de distribuição Qui-Quadrado:

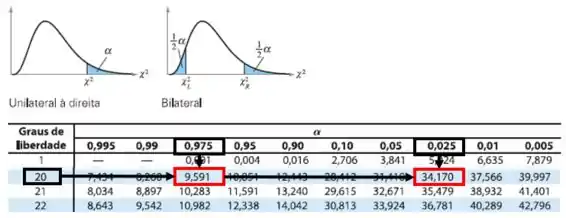
Então:

E:

Prontinho pessoal, esse foi rapidinho, bora para mais um exercício? Até mais!