Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 15
e jogam uma partida de “cara e coroa”, lançando cada um 50 moedas. vencerá o jogo se conseguir 5 ou mais caras do que e, quando isso não ocorrer, vencerá. Determinar as vantagens contra a vitória de em qualquer jogada particular.
Passo 1
Oi pessoal. Vamos pensar juntos neste exercício?! Iremos iniciar relembrando de algumas teorias.
A distribuição amostral de somas ou diferenças de duas proporções amostrais, é dada pela seguinte equação:
Pelo enunciado temos os seguintes dados:
- ;
- ;
- .
E queremos determinar as vantagens contra a vitória de A em qualquer jogada, e sabemos que A ganha se conseguir 5 ou mais caras que B. Sendo assim, temos o seguinte:
Então:
Pela tabela da distribuição normal é:
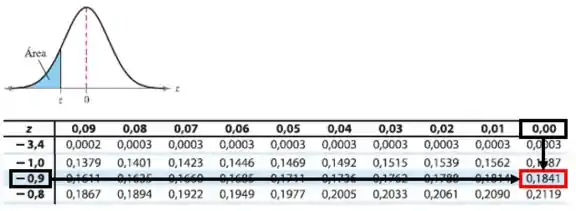
Tchau galerinha! Te espero em mais exercícios.
Resposta
.
Exercícios de Livros Relacionados
Um dado é jogado 600 vezes. Determinar a probabilidade de que o número de vezes em que sai face 1 , difira da média por mais que 30v e z e s .
O IBC determinou, a partir de várias experiências, que 5% das sementes de café não germinavam. Estas sementes são vendidas em pacotes de 400 unidades, com a garantia de que pelo menos 92% delas germin
Sabe-se que 20% das peças produzidas por umas siderúrgicas são defeituosas. Selecionando-se, ao acaso e com reposição, 100 peças da produção, qual a probabilidade de encontrarmos de 15 a 30 defeituosa
Numa indústria, 30% dos funcionários têm mais que 35a n o s . Selecionando-se, ao acaso e com reposição, 600 funcionários, qual a probabilidade de encontrarmos menos que 165 pessoas dessa faixa etária
Numa estrada, numa certa faixa de horários, passam em média 900 carros por hora, segundo uma distribuição de Poisson. Calcular a probabilidade de passarem, em 30 minutos, mais que 480c a r r o s .