Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 6.Exercícios propostos - Ex. 16

Comparar a distribuição de Poisson com média igual a 15, com distribuição normal de mesma média e variância.

Obs.: Trabalhar com 5 casas decimais.

Passo 1

Olá galerinha, vamos resolver mais um exercício juntos? Então vamos lá!

A distribuição de Poisson pode ser aproximada por uma Normal, desde que seja a média (que no caso da distribuição de Poisson é igual à variância) deve ser maior ou igual a 15. A correção de continuidade deve ser feita, pois a distribuição de Poisson é caracterizada para uma variável discreta. Tal correção consiste em considerar que a probabilidade de ocorrer um valor genérico na distribuição Binomial. Sendo assim, iremos calcular a probabilidade de ocorrer um valor entre e na distribuição Normal.

Neste exercício iremos utilizar a distribuição Normal e de Poisson, e pelo enunciado sabemos que:

Para a distribuição normal, sabemos que:

Sendo assim, conseguimos encontrar nosso valor :

Para :

Pela Tabela da distribuição Normal, temos:

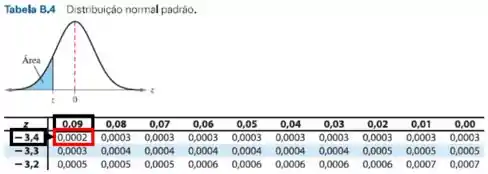
Passo 2

Já para o cálculo pela distribuição de Poisson, utilizamos a equação:

Fazendo o mesmo para , obtemos os resultados:

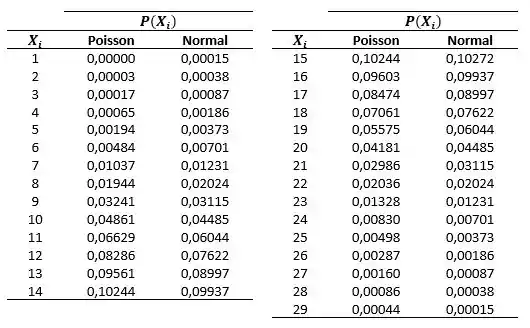
Tchau galerinha! Te espero em mais exercícios.

Resposta

Resposta no Passo 2.

Exercícios de Livros Relacionados

Certas válvulas produzidas por uma empresa têm vida média de 900 h e desvio padrão de 80 h. A empresa envia 1.000 lotes, de 100 válvulas cada um. Em quantos lotes pode-se esperar que:os desvios padrõe

Entre 1.000 amostras, de 200 crianças cada uma, em quantas esperar-se-ia encontrar:menos de 40% de meninos;53% ou mais de meninas.

Para uma distribuição de qui-quadrado com 12 graus de liberdade, determinar o valor de X c 2 de modo que:a área à direita desse ponto seja de 5%;a área à esquerda desse ponto seja de 99%.

Determinar os valores de t 1 , para a distribuição de Student, que satisfaçam cada uma das seguintes condições:área entre - t 1 e t 1 de 90%, com ϕ = 25 ;área à esquerda de - t 1 de 2,5%, com ϕ = 20 ;

Um fabricante faz a remessa de 1.000 lotes, de 100 parafusos cada um. Se 5% dos parafusos são normalmente defeituosos, em quantos lotes pode-se esperar que existam:menos que 90 parafusos perfeitos;98