Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 33

Determine a cor variância e a correlação para as seguintes distribuições de probabilidade conjuntos:

Passo 1

A distribuição de probabilidade conjunta dada é:

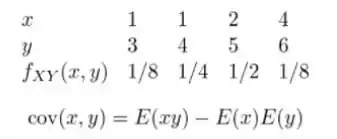
Letra a:

Precisamos calcular:

E ( X Y ) = 9.375

e

E ( X ) = 1.1875

e

E ( Y ) = 4.625

Então,

c o v ( X , Y ) = 9.375 - ( 1.875 ) ( 4.625 ) = 0.7031

Passo 2

Letra b:

ρ x = c o v ( X , Y ) V ( X ) V ( Y )

Agora temos que calcular as variâncias de X e Y.

V ( X ) = E ( X 2 ) - E ( X ) 2 =

= 0.8594

V ( Y ) = 0.7344

Então,

ρ x y = 0.7031 ( 0.894 ) ( 0.7344 ) = 0.885

Resposta

  1. 0.7031
  2. 0.885
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As v.a. X e Y têm distribuição conjunta dada por:Encontre as f.d.p. marginais de X e Y.
Mesmos itens do Problema 22 para a f.d.p. conjunta. f x ,y =3 e –x+3 y, x0 , y0 .
Suponha que as v.a. X e Y tenham f.d.p.Calcule P(0
As v.a. X e Y têm distribuição conjunta dada por:Faça um gráfico do domínio de variação de x e y.
As v.a. X e Y têm distribuição conjunta dada por:Prove que∬ f ( x ,y ) d x d y=1 .