Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 18c

As v.a. X e Y têm distribuição conjunta dada por:

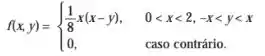
Encontre as f.d.p. marginais de X e Y.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para pegar o que aconteceu lá na combinação das variáveis e encontrar as f.d.p. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser analisar a definição. Para todos os valores de x entre 0 e 2, o y da função fica variando entre os valores associados ao x, acompanhando aquela função de reta dada ali. Para quaisquer outros números, a função vale zero. Então, com isso, já sabemos nossos limites de integração.

Bom, agora precisamos redefinir nossa função para uma forma que possamos trabalhar com ela.

f y =   ∫ y 2 1 8 x x - y d x   ,   0 < y < 2 ∫ - y 2 x x - y d x ,   - 2 < y < 0 0 ,   c c

f x =   ∫ - x x 1 8 x x - y d y ,   0 < x < 2 0 , c c

Passo 3

Pronto!! Agora é só calcular cada um dos casos!!

∫ y 2 1 8 x x - y d x =   1 48 ( y 3 - 12 y + 16 )

∫ - y 2 x x - y d x = 1 48 ( 5 y 3 - 12 y + 16 )

∫ - x x 1 8 x x - y d y = x 3 4

Resposta

∫ y 2 1 8 x x - y d x =   1 48 ( y 3 - 12 y + 16 )

∫ - y 2 x x - y d x = 1 48 ( 5 y 3 - 12 y + 16 )

∫ - x x 1 8 x x - y d y = x 3 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a marca de referência do Conselho de desempenho do processamento da transação do exercício. 10, sejam X, Y e Z e o número médio de operações que seleciona, atualiza e insere requerido para cada t
10-34. Um artigo no Journal of Aircrafi (Vol. 23. 1986. p. 859 864desereve uma nova formulaçào do método de análise de placa equiva.lente, que é capaz de modclar estruturas de aviocs. tais comks vigas
10-42. Considere o teste de hipóteses, contra Suponha quc os tamanhos de amostra sejam n, - 20 e n, = S e que. Use Teste a hipótese e explique como oteste pexleria ser conduzido com um intervalo de co
10-41. Considere o leste de hipóteses Ha: contra H: Suponha que os tamanhos de amostra sejam n, - 5 e n. = 10 e queUse, Teste a hipotese e explique comeotesle podena ser conduzido com uin intervalo de
10-38. Em Biomctrics(1990. Vol. 46. pp.673-87).os autores analisa-ram a circunferencia de cinco laranjeiras (marcada como A-E), medi-das em sete cxasioes (x).a)Comparc o aumento medio na circunferénei