Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 43

A distribuição de probabilidade conjunta é.

Mostre que a correlação entre X e Y é zero, porém X e Y não são independentes.

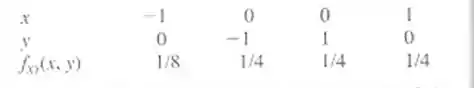
Passo 1

Temos dado, a distribuição de probabilidade conjunta:

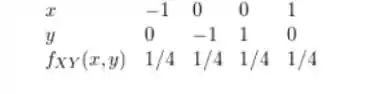
Então,

E ( X ) = ∑ x   x p x ( x ) = - 1 ⋅ 1 4 + 0 ⋅ 1 4 + 0 ⋅ 1 4 + 1 ⋅ 1 4 = - 1 4 + 1 4 = 0 E ( Y ) = ∑ y   y p y ( y ) = 0 ⋅ 1 4 + ( - 1 ) ⋅ 1 4 + 1 ⋅ 1 4 + 0 ⋅ 1 4 = - 1 4 + 1 4 = 0

E X 2 = ∑ x 2 P x ( x ) = ( - 1 ) 2 1 4 + 0 2 1 4 + 0 2 1 4 + 1 2 1 4 = 1 4 + 1 4 = 1 2 E Y 2 = ∑ y = 0 4   y 2 p Y ( y ) = ( 0 ) ⋅ 1 4 + ( - 1 ) 2 ⋅ 1 4 + ( 1 ) 2 ⋅ 1 4 + 0 2 ⋅ 1 4 = 1 4 + 1 4 = 1 2

E ( X Y ) = ∑ x   ∑ y   x y P X Y ( x , y ) = - 1 ⋅ 0 ⋅ 1 4 + 0 ⋅ ( - 1 ) ⋅ 1 4 + 0 ⋅ 1 ⋅ 1 4 + 1 ⋅ 0 ⋅ 1 4 = 0

V ( X ) = E X 2 - [ E ( X ) ] 2 = 1 2 - 0 = 1 2 V ( Y ) = E Y 2 - [ E ( Y ) ] 2 = 1 2 - 0 = 1 2 c o v ⁡ ( X , Y ) = E ( X Y ) - E ( X ) E ( Y ) = 0 - 0 ⋅ 0 = 0 c o r r ⁡ ( X , Y ) = 0 1 2 1 2 = 0

Passo 2

Mesmo que a correlação seja 0, não vamos concluir que X e Y são independentes.

Se X e Y forem independentes, então f X Y ( x , y ) = f ( x ) × f ( y )

f ( 1,1 ) = 0 f ( 1 ) ⋅ f ( 1 ) = 1 4 ⋅ 1 4 = 1 16 ≠ f ( 1,1 ) f ( 1,0 ) = 1 4 f ( 1 ) ⋅ f ( 0 ) = 1 4 ⋅ 1 2 = 1 8 ≠ f ( 1,0 )

Conseqüentemente, podemos concluir que X e Y não são independentes, embora a correlação é 0.

Resposta

Conseqüentemente, podemos concluir que X e Y não são independentes, embora a correlação é 0.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os pesos de tijolos de barro usadas em construção são distribuídas normalmente, com uma média de três libras e o desvio padrão de 0.25 libras. Suponha que os pesos dos tijolos sejam independentes e qu
Determine o valor de c, a covariância e a correlação para função de probabilidade conjunta
Determine o valor de ser Equi torna uma função densidade de probabilidade conjunta sobre a região. Determine o seguinte:
Suponha que é correlação entre X e Y seja P. Para as constantes a, b, c e d qual é a correlação entre as variáveis aleatórias