Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 29

Determine o valor de ser Equi torna uma função densidade de probabilidade conjunta sobre a região. Determine o seguinte:

Passo 1

A função de densidade de probabilidade conjunta é dada como:

f X Y Z ( x , y , z ) = c ,   x > 0 , y > 0 , x + y + z < 1

f X Y Z ( x , y , z ) = 0 ,   e m   o u t r o   c a s o .

Seja X uma variável aleatória unidimensional com função de densidade de probabilidade f X , a função de densidade de probabilidade deve satisfazer o seguinte:

∫ - ∞ ∞ f X ( x ) d x = 1

Da mesma forma, para a variável aleatória tridimensional com densidade de probabilidade função f X Y Z , temos:

∫ - ∞ ∞ ∫ - ∞ ∞ ∫ - ∞ ∞ f X Y Z ( x , y , z ) d x d y d z = 1

Para calcular a constante c, usaremos a propriedade acima:

∫ - ∞ ∞ ∫ - ∞ ∞ ∫ - ∞ ∞ f X Y Z ( x , y , z ) d x d y d z =

=   ∫ 0 1 ∫ 0 1 - x ∫ 0 1 - x - y c d x d y d z =

= c ∫ 0 1 ∫ 0 1 - x ( 1 - x - y ) d y d x =

= c ∫ 0 1 ( ∫ 0 1 - x d y - x ∫ 0 1 - x d y - ∫ 0 1 - x y d y ) d x =

= c ∫ 0 1 ( y 1 - x 0 - x y 1 - x 0 + - 1 2 y 2 1 - x 0 ) d x =

= c ∫ 0 1 ( ( 1 - x ) - x ( 1 - x ) - 1 2 ( 1 - x ) 2 ) d x =

= c ∫ 0 1 ( 1 - x - x + x 2 - ( 1 - x ) 2 2 ) d x =

= c ∫ 0 1 ( ( 1 - x ) 2 - ( 1 - x ) 2 2 ) d x =

= c 2 ∫ 0 1 ( 1 - x ) 2 d x =

= c 2 ( x - x 2 + 1 3 x 3 ) 1 0 = c 6

Aqui temos que manter o controle dos limites. Se você alterar a ordem limite da integração pode mudar! A função de densidade de probabilidade é 0 para outros valores. A área que estamos integrando é a área entre três planos, veja a imagem abaixo.

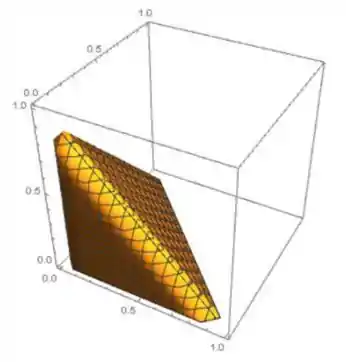
Agora temos que c 6 = 1 , o que significa que c=6. A função de probabilidade de densidade é na verdade:

f X Y Z ( x , y , z ) = 6 ,   x > 0 , y > 0 , x + y + z < 1

f X Y Z ( x , y , z ) = 0 ,   e m   o u t r o   c a s o .

Passo 2

Letra a:

Vamos ver qual é a probabilidade P ( X < 0.5 ,   Y < 0.5 ,   Z < 0.5 ) . Quando desenhamos as superfícies x = 0.5 ,   y = 0.5 ,   z = 0.5 com as condições acima, temos um cubo com o comprimento de uma aresta 0.5. A integral vai realmente ser o volume do cubo, que é 0.5 × 0.5 × 0.5 = 0.125 menos o volume de uma pirâmide triangular com volume V = B × H , onde B = a 2 3 4 , H 2 = a 2 - ( a 3 ) 2 3 2 e a = 0.5 por causa da condição x + y + z < 1 . Então:

P ( X < 0.5 , Y < 0.5 < Z < 0.5 ) =

= 6 ∫ 0 1 ∫ 0 1 - x ∫ 0 1 - x - y d z d y d x =

≈ 6 × ( 0.125 - 0.018 ) ≈

≈   0.64

Passo 3

Letra b:

Para a probabilidade P ( X < 0.5 ,   Y < 0.5 ) , calculamos a integral. Assim temos:

P ( X < 0.5 , Y < 0.5 ) =

= 6 ∫ 0 1 ∫ 0 1 - x ∫ 0 1 - x - y d z d y d x =

= 6 ∫ 0 0.5 ∫ 0 0.5 ( 1 - x - y ) d y d x =

= 6 ∫ 0 0.5 ( y - x y - 1 2 y 2 ) | 0.5 0 d x =

= 6 ∫ 0 0.5 ( ( 0.5 - 0 ) - x ( 0.5 - 0 ) - 1 2 ( ( 0 . 5 2 ) - 0 2 ) ) d x =

= 6 ∫ 0 0.5 0.375   -   0.5 x   d x =

= ( 2.25 x - 3 2 x 2 ) 0.5 0 =

= 1.125 - 0.375 =

= 0.75

Passo 4

Letra c:

Vamos encontrar a probabilidade P ( X < 0.5 ) :

P ( X < 0.5 ) = 6 ∫ 0 0.5 ∫ 0 1 - x ∫ 0 1 - x - y d z d y d x =

= 3 ∫ 0 0.5 ( 1 - x ) 2 d x =

= 3 ( x - 2 2 x 2 + 1 3 x 3 ) 0.5 0 = 0.875

Passo 5

Letra d:

Vamos encontrar a expectativa E ( X ) . Aqui, precisamos calcular a distribuição marginal para X. Calculamos as funções de densidade marginal:

f X ( x ) = ∫ - ∞ ∞ ∫ - ∞ ∞ f X Y Z ( x , y , z ) d y d z

Uma vez que as variáveis ​​aleatórias que recebemos são contínuas, porque temos função de densidade conjunta que é uma função contínua, calculamos as expectativas como:

E ( X ) = ∫ - ∞ ∞ x f X ( x ) d x

Combinando esses dois, e olhando na área de definição, temos:

E ( X ) = 6 ∫ 0 1 ∫ 0 1 - x ∫ 0 1 - x - y x d z d y d x =

= 3 ( 1 2 x 2 - 2 3 x 3 + 1 4 x 4 ) 1 0 = 0.25

Passo 6

Letra e:

Temos a definição de distribuição marginal acima. Usando a definição para x ∈ ( 0,1 )

f X ( x ) = 6 ∫ 0 1 - x ∫ 0 1 - x - y d z d y d x = 3 ( 1 - x ) 2

Para x < 0   e   x > 1 a função é 0. A função de densidade de probabilidade marginal é:

f X ( x ) = 3 ( 1 - x ) 2 ,   x ∈ ( 0,1 )

f X ( x ) = 0 ,   e m   o u t r o   c a s o .

Passo 7

Letra f:

Vamos calcular a distribuição conjunta de X e Y como a distribuição de probabilidade marginal conjunta f X Y Z . Então, pela definição, para x > 0 ,   y > 0   e x + y < 1 :

f X Y ( x , y ) = 6 ∫ 0 1 - x - y d z = 6 ( 1 - x - y )

não se esqueça de verificar qual é a função x e y conforme abaixo. Para outro x e y, a função de probabilidade conjunta f X Y Z   é 0, assim como f X Y . Então, a distribuição conjunta de X e Y é:

f X Y ( x , y ) = 6 ( 1 - x - y ) ,   x > 0 ,   y > 0 ,   x + y < 1

f X Y ( x , y ) = 0 ,   e m   o u t r o   c a s o .

Passo 8

Letra g:

Para encontrar a distribuição de probabilidade condicional de X, dado que Y = 0.5 e Z = 0.5, precisamos de:

f X | Y = y , Z = z ( x ) = f X Y Z ( x , y , z ) f Y Z ( y , z )

Como Y = 0.5 e Z = 0.5, x + y + z < 1 não é satisfeito para cada x > 0 , o que significa f X y z   ( x , y , z ) = 0 , então a distribuição de probabilidade condicional de X dado que Y = 0.5 e Z = 0.5 será 0.

Passo 9

Letra h:

Usando a definição da função de densidade condicional:

f X | Y = y ( x ) = f X Y ( x , y ) f Y ( y )

e o fato de que podemos calcular a distribuição marginal de Y da mesma maneira quanto para X:

f Y ( y ) = 3 ( 1 - y ) 2 ,   y ∈ ( 0,1 )

f Y ( y ) = 0 ,   e m   o u t r o   c a s o .

podemos usar os resultados que temos acima e calcular para x > 0 e x < 0.5 :

f X | Y = 0.5 ( x )

= f X Y ( x , 0.5 ) f Y ( 0.5 ) =

= 4 ( 1 - 2 x )

para todos os outros x, a distribuição de probabilidade condicional de X, dado que Y =

0.5 é 0. Finalmente, a distribuição de probabilidade condicional de X, dado que Y = 0.5 é:

f X | Y = 0.5 ( x ) = 4 ( 1 - 2 x ) ,   x ∈ ( 0,0.5 )

f X | Y = 0.5 ( x ) = 0 ,   e m   o u t r o   c a s o .

Resposta

  1. 6
  2. 0.64
  3. 0.75
  4. 0.875
  5. 0.25
  6. f X ( x ) = 3 ( 1 - x ) 2 ,   x ∈ ( 0,1 )

    7. f X ( x ) = 0 ,   e m   o u t r o   c a s o .

  7. f X Y ( x , y ) = 6 ( 1 - x - y ) ,   x > 0 ,   y > 0 ,   x + y < 1

    8. f X Y ( x , y ) = 0 ,   e m   o u t r o   c a s o .

  8. 0
  9. f X | Y = 0.5 ( x ) = 4 ( 1 - 2 x ) ,   x ∈ ( 0,0.5 )

f X | Y = 0.5 ( x ) = 0 ,   e m   o u t r o   c a s o .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a cor variância e a correlação para distribuição de probabilidade de conjuntos mostrados na figura 5.4 e descrito no exemplo se.6
Determine a covariância e a correlação para a seguinte distribuição de probabilidades conjuntas
Determine o valor de c, a covariância e a correlação para a função densidade de probabilidade conjunta f x y x , y = c x y para a faixa de 0x3 e 0yx .
Suponha que as variáveis ​​aleatórias X, Y e 2 tenham a função de densidade de probabilidade conjunta sobre o cilindro .r2 y2 Determine o seguinte:
Determine a cor variância e a correlação para as seguintes distribuições de probabilidade conjuntos: