Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 1a

Lançam-se, simultaneamente, uma moeda e um dado.

(a) Determine o espaço amostral correspondente a esse experimento.

(b) Obtenha a tabela da distribuição conjunta, considerando X o número de caras no lançamento da moeda e Y o número da face do dado.

(c) Verifique se X e Y são independentes.

(d) Calcule:

1. P ( X = 1 )

2.   P ( X ≤ 1 )

3. P ( X < 1 )

4. P X = 2 ,     Y = 3

5. P ( X ≥ 0 ,     Y ≤ 4 )

6. P ( X = 0 ,     Y ≥ 1 )

Passo 1

(a) Determine o espaço amostral correspondente a esse experimento.

Queremos o espaço amostral ( Ω ). Vamos olhar separadamente:

  • Quando lançamos uma moeda temos dois possíveis resultados: cara (C) ou coroa (R). Logo, o espaço amostral é Ω 1 = { C ,   R } .

  • Quando lançamos um dado temos seis possíveis resultados: 1, 2, 3, 4, 5 e 6. Logo, o espaço amostral é Ω 2 = 1 ,   2 ,   3 ,   4 ,   5 ,   6 .

Portanto, o espaço amostral são as possibilidades de combinação desses dois conjuntos, correto?

Ω = { ( C , 1 ) ,   ( C , 2 ) ,   ( C , 3 ) ,   ( C , 4 ) ,   ( C , 5 ) ,   ( C , 6 ) ,   ( R , 1 ) ,   ( R , 2 ) ,   ( R , 3 ) ,   ( R , 4 ) ,   ( R , 5 ) ,   ( R , 6 ) }

Passo 2

(b) Obtenha a tabela da distribuição conjunta, considerando X o número de caras no lançamento da moeda e Y o número da face do dado.

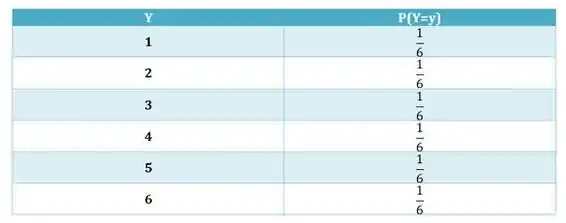
Queremos montar uma tabela considerando X = número de caras (C) no lançamento da moeda e Y = número da face do dado.

Analisando X :

Analisando Y :

Passo 3

Montando a nossa tabela, temos:

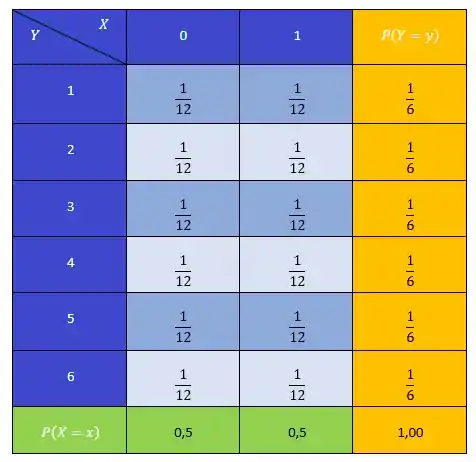
Passo 4

(c) Verifique se X e Y são independentes.

Sim, pois P X = i ,   Y = j = P X = i P Y = j ,   ∀ i ,   j

Passo 5

(d) Vamos calcular algumas probabilidades:

1. P X = 1

Como X é o número de caras no lançamento do dado, queremos a probabilidade de obter uma cara, ou seja

P X = 1 = 1 2

2. P X ≤ 1

Como X é o número de caras no lançamento do dado, queremos a probabilidade de dois casos: X = 0 → N ã o   s a i r   c a r a ou P X = 1 → S a i r   c a r a . Ou seja, estamos falando das duas possíveis ocorrências ao lançar uma moeda, portanto:

P ≤ 1 = 1

3. P X < 1

Como X é o número de caras no lançamento do dado, queremos a probabilidade de X < 1 , ou seja, de X = 0 → N ã o   s a i r   c a r a .

P X < 1 = P X = 0 = 1 2

4. P X = 2 ,   Y = 3

Opa! Queremos saber a probabilidade de X = 2 ! Mas isso não existe, certo? Afinal, a moeda é lançada apenas uma vez, logo, não é possível obter duas caras!

P X = 2 ,   Y = 3 = 0

5. P X ≥ 0 ,   Y ≤ 4

Primeira coisa que devemos olhar são quais eventos estão aí dentro:

- P X ≥ 0 = P X = 0 + P X = 1 → t o d a s   a s   p o s s i b i l i d a d e s

-   P Y ≤ 4 = P Y = 1 + P Y = 2 + P Y = 3 + P ( Y = 4 )

Então queremos

P X = 0 ,   Y = 1 + P X = 0 ,   Y = 2 + P X = 0 ,   Y = 3 + P X = 0 ,   Y = 4 +

+ P X = 1 ,   Y = 1 + P X = 1 ,   Y = 2 + P X = 1 ,   Y = 3 + P ( X = 1 ,   Y = 4 )

Pela tabela é fácil de localizar cada um desses termos, por exemplo:

P X = 0 ,   Y = 1 → 2 °   t e r m o   d a   2 a   c o l u n a → 1 12

Assim

P X ≥ 0 ,   Y ≤ 4 = 8 × 1 12 = 2 3

6. P X = 0 ,   Y ≥ 1

Agora, vamos olhar apenas para os casos onde X = 0   e   Y ≥ 1 .

Seguindo o mesmo raciocínio do item anterior, temos:

P X = 0 ,   Y ≥ 1 = P X = 0 ,   Y = 1 + … + P X = 0 ,   Y = 6

Pela tabela novamente localizarmos esses termos, logo:

P X = 0 ,   Y ≥ 1 = 6 × 1 12 = 1 2

Resposta

(a) Ω = { ( C , 1 ) ,   ( C , 2 ) ,   ( C , 3 ) ,   ( C , 4 ) ,   ( C , 5 ) ,   ( C , 6 ) ,   ( R , 1 ) ,   ( R , 2 ) ,   ( R , 3 ) ,   ( R , 4 ) ,   ( R , 5 ) ,   ( R , 6 ) }

(b)

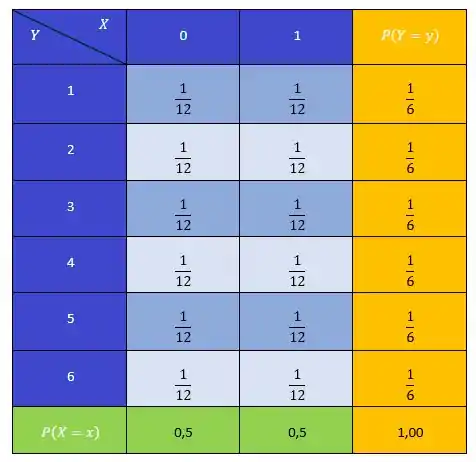
(c) Sim, pois P X = i ,   Y = j = P X = i P Y = j ,   ∀ i ,   j .

(d)

1. 1 2

2. 1

3. 1 2

4. 0

5. 2 3

6. 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A função de probabilidade conjunta entre as variáveis aleatórias X e Y é apresentada na próxima tabela.Obtenha as tabelas marginais de frequência.X e Y são independentes?Calcule a covariância e a corr
A função de probabilidade conjunta entre as variáveis aleatórias X e Y é apresentada na próxima tabela.Obtenha as tabelas marginais de frequência.X e Y são independentes?Calcule a covariância e a corr
Uma amostra de 220 clientes de uma clínica dentária foi selecionada. As variáveis tempo, em anos, decorridos desde a última visita ao dentista (V) e o número de cáries encontradas (C) é apresentado na
Na caixa I existem duas bolas numeradas 0 e 1, enquanto que a caixa II contêm duas bolas numeradas 1 e 0. Uma bola é retirada aleatoriamente de cada caixa, de forma independente uma da outra. A esse e
A variável X é Bernoulli com p :0,4 e Y é Binomial com p :0,5en :3 . Admita que XeY são independentes.Determine P X = 0 Y = 2 . Obtenha a função de probabilidade conjunta do X e Y e do produto XY.Calc