Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios - Ex. 25
Dor leve nas costas (DLC) é um problema de saúde sério em muitos ambientes industriais. O artigo "Isodynamic Evaluation of Trunk Muscles and Low-Back Pain Among Workers in a Steel Factory" (Ergonomics, 1995, p. 2107-2117) relatou os dados resumidos a seguir sobre o intervalo de movimentos laterais (graus) para uma amostra de trabalhadores sem um histórico de DLC e para outra amostra com histórico dessa doença.
Passo 1
Temos que m=28 e n=31 são tamanhos de amostra, e que são variáveis aleatórias normais independentes e identicamente distribuídas (temos que usar a suposição de normalidade para prosseguir com a construção de um intervalo de confiança) com média e desvio padrão , ambos desconhecidos (estes representam a amplitude de movimento lateral para pessoas sem lombalgia).
Também nos é dado que são variáveis aleatórias normais independentes e identicamente distribuídas (temos que usar a suposição de normalidade aqui também) com média e desvio padrão , ambos desconhecidos (estes representam a amplitude de movimento lateral para pessoas com lombalgia).
Além disso, X e Y são amostras independentes (portanto, todos os são independentes de todos os).
Lembre-se de que um intervalo de confiança para é da forma
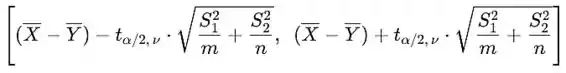
Onde é um valor tal que a área sob a curva de densidade da distribuição t com graus de liberdade, à direita desse valor, é igual a .
Em primeiro lugar, os graus de liberdade são calculados como
Passo 2
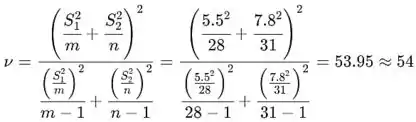
Agora podemos usar a Tabela A.5 nas Tabelas do Apêndice para encontrar aproximadamente. Nós olhamos sob a linha rotulada com (já que não há linha para , e este é o mais próximo de 54) e a coluna rotulada com α=0.05. O valor desejado está localizado no corpo da tabela, sob essa linha e coluna, e podemos descobrir que é ≈1.676.
Passo 3
Então, substituindo todos os valores dados, , = 88.3, , na fórmula para o intervalo de confiança de 90%, dado acima, nos dá o intervalo de confiança de 90% desejado para
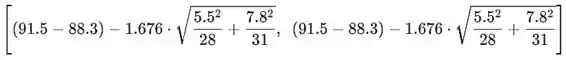
Como esse intervalo de confiança não contém o valor 0, podemos estar razoavelmente (90\%90%) certos de que o movimento lateral médio da população real é diferente para as duas condições (porque 0 não é um valor plausível para ou seja, não é plausível que ).
Suponha agora que queremos um intervalo de confiança de 95% para . A única coisa que muda é o quantil , pois agora precisamos de .
Ele pode ser encontrado aproximadamente usando a tabela A.5 nas Tabelas do Apêndice.
Nós olhamos sob a linha rotulada com (já que não há linha para ν=54, e este é o mais próximo de 54) e a coluna rotulada com α=0.025. O valor desejado é então localizado no corpo da tabela, sob essa linha e coluna, e podemos descobrir que é
Então, substituindo todos os valores dados, , , na fórmula para o intervalo de confiança de 95%, dado acima, nos dá o intervalo de confiança de 95% :
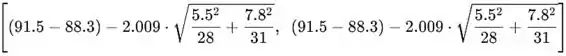
Como esse intervalo de confiança agora contém o valor 0, então 0 é um candidato plausível para o valor verdadeiro de , ou seja, não podemos rejeitar a possibilidade de que o movimento lateral médio da população verdadeira seja o mesmo para as duas condições.
Resposta
O intervalo de confiança de 90% é [0,276,6,124], e não contém o valor 0.
O intervalo de confiança de 95% é [−0,305,6,705] e contém o valor de 0