Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 9.Exercícios propostos - Ex. 12

Uma amostra com, n 1 = 25   e l e m e n t o s , foi extraída de uma população normal, dando média 80. Numa segunda amostra, com n 2 = 36   e l e m e n t o s , de uma outra população normal, deu média 75. Determinar o intervalo de confiança, ao nível de 96%, para μ 1 - μ 2 . Os desvios padrões das populações são de 5 e 3, respectivamente.

Passo 1

Oi galera, vamos lá!

O valor da probabilidade ( 1 - α ), que usualmente assume os valores 90%, 95%, 98%, etc., é denominado nível de confiança e o valor α é chamado nível de significância.

Para o intervalo de confiança para a soma e para a diferença entre duas médias ( μ 1 e μ 2 ) de duas populações normais, quando as variâncias ( σ 1 2 σ 2 2 ) são conhecidas, temos a seguinte equação para amostras aleatórias independentes:

( X - 1 ± X - 2 ) - z α / 2 ∙ σ 1 2 n 1 + σ 2 2 n 2 ≤ ( μ 1 ± μ 2 ) ≤ ( X - 1 ± X - 2 ) + z α / 2 ∙ σ 1 2 n 1 + σ 2 2 n 2

Do enunciado, temos os seguintes dados:

  • n 1 = 25 ;
  • X - 1 = 80 ;
  • σ 1 = 5 ;
  • n 2 = 36 ;
  • X - 2 = 75 ;
  • σ 2 = 3 ;
  • α = 0,04

Para um nível de confiança de 96%:

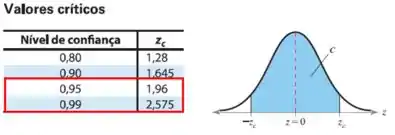
Podemos perceber que não temos o valor de 0,96, então iremos realizar uma interpolação:

z c - 1,96 2,575 - 1,96 = 0,96 - 0,95 0,99 - 0,95

z c = 2,1

Passo 2

Sendo assim, para o nível de confiança de 96%:

( μ 1 - μ 2 ) = ( 80 - 75 ) ± 2,1 ∙ 5 2 25 + 3 2 36

2,7 ≤ μ 1 - μ 2 ≤ 7,3

Tchau galerinha! Te espero em mais exercícios.

Resposta

2,7 ≤ μ 1 - μ 2 ≤ 7,3 .

Exercícios de Livros Relacionados

Considere os dados a seguir sobre a carga de quebra (kg/25 mm de largura) de vários tecidos em uma condição não-friccionada e uma condição friccionada ("The Effect of Wet Abrasive Wear on the Tensile
Consulte o Exercício 34. Descreva o teste combinado t para testar H0: 1 2 0 quando ambas as distribuições das populações são normais 1 2. Então, use esse procedimento de teste para testar as hipóteses
O artigo citado no Exercício 34 na Seção 7.3 forneceu os dados resumidos a seguir sobre os limites de tensão proporcionais dos espécimes construídos, usando dois tipos diferentes de madeira:Assumindo
Suponha que μ 1 e μ 2 sejam distâncias de parada médias reais em 50 mph de certo tipo de carros equipados com dois tipos diferentes de sistemas de frenagem. Use o teste t de duas amostras no nível de
Use os dados do Exercício 19 para calcular um IC de 95% para a diferença entre a distância de parada média real dos carros equipados com o sistema 1 e dos carros equipados com o sistema 2. O intervalo