Enunciado

Probabilidade e Estatística - Probabilidade, um curso moderno com aplicações, de Sheldon Ross- Ed: 8º - Capítulo 1.Problemas - Ex. 7d

E se duas pessoas do mesmo sexo não

puderem se sentar juntas?

Passo 1

Opa galeeeeera! Hoje vamos entender mais um pouco sobre o Principio Fundamental da Contagem (PFC).

Aqui temos 3 garotos e 3 garotas e há a restrição de que pessoas do mesmo sexo não podem estar juntas. Então vamos raciocinar um pouco.

Lembre-se que se não podemos colocar pessoas do mesmo sexo juntas, ao escolher um menino para estar em uma posição, necessariamente ao lado dele só estarão meninas.

Vamos imaginar essas 6 posições que essas 6 pessoas vão sentar:

E ir colocando uma a uma respeitando as condições de que não podemos colocar um menino e uma menina um ao lado do outro.

Passo 2

Para a primeira pessoa dessa fila podemos escolher qualquer uma das 6 pessoas, então há 6 possibilidades (3 meninos + 3 meninas).

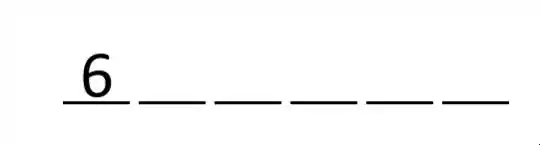
Essa pessoa escolhida pode ser de qualquer sexo. Caso ela seja menino a pessoa ao lado tem que ser menina, e existem necessariamente 3 meninas.

E analogamente, caso essa primeira pessoa seja menina restarão 3 meninos para serem escolhidos para ser colocado ao lado dela. Assim há necessariamente 3 formas de se escolher esta segunda pessoa.

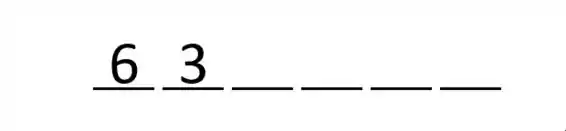
Passo 3

Agora para a 3ª pessoa, basta lembrarmos que das seis pessoas necessariamente um menino e uma menina já foram escolhidos, então sobraram quatro pessoas que ainda não estão na fila. Sendo 2 meninos e 2 meninas.

Lembrando que nenhuma pessoa pode ser do mesmo sexo que a pessoa ao seu lado vamos ter 2 possibilidades para este 3º lugar, independentemente do segundo ser menino ou menina.

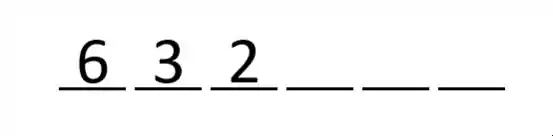
Seguindo o raciocínio análogo do passo anterior, tinham 2 meninos e 2 meninas restando antes de escolher esta 3ª pessoa, e independente de quem eu escolher, o próximo será do sexo oposto onde só há 2 possibilidades.

Então para a 4ª posição há 2 possibilidades.

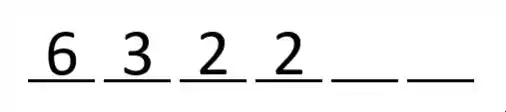
Passo 4

Agora já foram escolhidos dois meninos e duas meninas, restando somente um menino e uma menina.

Para a 5ª posição podemos escolher somente a pessoa de sexo oposto a da posição, restando apenas uma possibilidade.

E como só restou uma pessoa, só há uma possibilidade para o último lugar.

Passo 5

Como tivemos que escolher a primeira pessoa e a segunda pessoa ... e a quinta pessoa e a sexta pessoa, pelo PFC precisamos multiplicar todas as possibilidades de cada colocação para obter o número total de possibilidades: