Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 2.Exercícios - Ex. 13

Uma empresa de consultoria em informática apresenta suas propostas de três projetos. Represente por A i = {projeto i fechado}, para i = 1,2 , 3 e suponha que P A 1 = 0,22 ,   P A 2 = 0,25 ,   P A 3 = 0,28 ,   P ( A 1 ∩ A 2 ) = 0,11 ,   P A 1 ∩ A 3 = 0,05 ,   P A 2 ∩ A 3 = 0,07 , P A 1 ∩ A 2 ∩ A 3 = 0,01 . Expresse em palavras cada evento a seguir e calcule sua probabilidade

a. A 1 ∪ A 2 b. A 1 ' ∩ A 2 ' Sugestāo: A 1 ∪ A 2 ' = A 1 ' ∩ A 2 ' ]

c. A 1 ∪ A 2 ∪ A 3 d. A 1 ' ∩ A 2 ' ∩ A 3 ' e. A 1 ' ∩ A 2 ' ∩ A 3 f. A 1 ' ∩ A 2 ' ∪ A 3

Passo 1

a. premiado com #1 ou #2 (ou ambos):

P A 1 ∪ A 2 = P A 1 + P A 2 - P A 1 ∩ A 2 = 22 + 25 - . 11 = 36

Passo 2

b. premiado com #1 ou #2 :

P A 1 * ∩ A 2 * = P A 1 ∪ A 2 ' = 1 - P A 1 ∪ A 2 = 1 - 36 = 64

Passo 3

c. recebeu pelo menos um dos # 1, # 2, # 3 :

P A 1 ∪ A 2 ∪ A 3 = P A 1 + P A 2 + P A 3 - P A 1 ∩ A 2 - P A 1 ∩ A 3 -

P A 2 ∩ A 3 + P A 1 ∩ A 2 ∩ A 3

=.22+.25+.28-.11-.05-.07+.01=53

Passo 4

d. não premiou nenhum dos três projetos:

P A 1 ' ∩ A 2 ' ∩ A 3   ' = 1 - P ( premiado pelo menos um ) = 1 - 53 = 47

Passo 5

e. premiado com # 3 mas nem # 1 nem # 2 :

P A 1 ' ∩ A 2 ' ∩ A 3 = P A 3 - P A 1 ∩ A 3 - P A 2 ∩ A 3

+ P A 1 ∩ A 2 ∩ A 3

= 28 - . 05 - 07 + . 01 = . 17

Passo 6

f. ou (nem #1 nem #2) ou #3:

P A 1 * ∩ A 2 * ∪ A 3 = P(região sombreada)=P(nenhuma premiada)+ P A 3   = 47 + 28 = . 75

Alternativamente, as respostas para a -f podem ser obtidas a partir de probabilidades no diagrama de Venn que acompanha

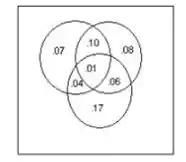
Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Uma universidade tem 10 mil alunos dos quais 4 mil são considerados esportistas. Temos, ainda, que 500 alunos são do curso de biologia diurno, 700 da biologia noturno, 100 são esportistas e da biologi
Uma universidade tem 10 mil alunos dos quais 4 mil são considerados esportistas. Temos, ainda, que 500 alunos são do curso de biologia diurno, 700 da biologia noturno, 100 são esportistas e da biologi
Sejam A e B dois eventos em um dado espaço amostral, tais que P A = 0 , 2 , P B = p , P A ∪ B = 0,5 e P A ∩ B = 0,1 . Determine o valor de p .
Verifique se são válidas as afirmações:Se P A = 1 / 3 e P B A = 3 / 5 então A e B não podem ser disjuntos.
Verifique se são válidas as afirmações:Se P A = 1 / 2 e P B A = 1 e P A B = 1 / 2 então A não pode estar contido em B .