Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 14.Exercícios propostos - Ex. 10b
Uma empresa fez um levantamento, mês a mês, durante os meses de um certo ano, a respeito de seu lucro líquido mensal , expresso em Cr$ 100.000,00, em função de seus gastos com propaganda em televisão e em rádio , ambos expressos em Cr$ 1.000,00.
Efetuando o cálculo dos somatórios necessários à montagem da regressão obteve:
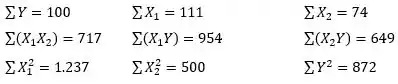
Pede-se:
- Dar a equação da regressão linear múltipla.
Passo 1
Olá galerinha, tudo bem com vocês? Primeiramente iremos relembrar a teoria.
A regressão linear múltipla é a regressão em que sabemos como variáveis contribuem para a realização do fenômeno, e a parte funcional da regressão é uma função linear. Onde a estimativa da equação de regressão é dada por:
Onde as estimativas , , , , dos coeficientes , , , , podem ser calculadas pelo método dos mínimos quadrados, partindo de hipóteses análogas aquelas adotadas pela regressão linear simples.
Para o caso de ter apenas duas variáveis explicativas:
Para encontrarmos os valores de , e , iremos utilizar as equações:
Onde iremos precisar calcular aas médias (, e ) pelas seguintes equações:
As variâncias vamos usar as equações:
E as covariâncias:
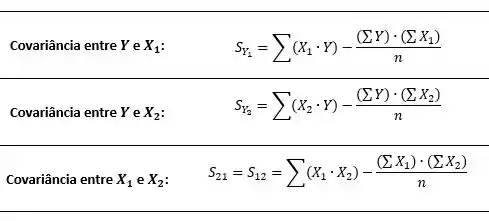
Passo 2
Então vamos para o nosso exercício. Do enunciado temos os seguintes dados:
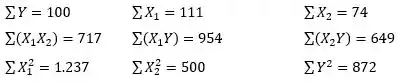
Primeiramente, vamos calcular as médias de , e , respectivamente:
Agora iremos calcular as variâncias:
E as covariâncias:
Passo 3
No item b), já queremos a equação da regressão simples, então precisamos calcular os valores de , e :
A equação da regressão linear múltipla:
Prontinho pessoal, até mais!
Resposta
.