Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 3.Exercícios - Ex. 26
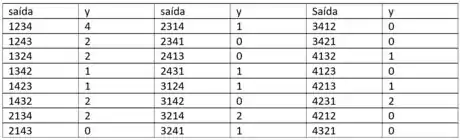
Depois que todos os estudantes saírem da sala de aula, um professor de estatística observa que quatro cópias do livro foram deixadas sob as mesas. No começo da próxima aula, o professor distribui os quatro livros de forma completamente aleatória para cada um de quatro alunos (1, 2, 3 e 4) que dizem ter esquecido os livros. Um resultado possível é que 1 receba o livro de 2, 2 receba o livro de 4, 3 receba o seu livro e 4 receba o livro de l. Esse resultado pode ser abreviado como (2, 4, 3, 1).
a. Relacione os outros 23 resultados possíveis.
b. Seja X o número de estudantes que recebem o próprio livro. Determine a fmp de X.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- O espaço amostral consiste em todas as permutações possíveis dos quatro números 1, 2, 3, 4:
- Então , , , ,
Passo 2
Resposta
Ver a resolução.
Exercícios de Livros Relacionados
Estima-se que 4.000 entre 10.000 eleitores moradores de uma cidade sejam contra o novo imposto sobremercadorias. Se 15 eleitores qualificados forem selecionados aleatoriamente e forem pedidas suas opi
Uma indústria de produtos eletrônicos afirma quea proporção de itens defeituosos de um processo éde 5% . Um comprador tem o procedimento padrão deinspecionar 15 unidades selecionadas aleatoriamentede
Uma empresa de extração de petróleo se arrisca emvários locais, e seu sucesso ou fracasso varia de um localpara outro. Suponha que a probabilidade de um sucessoem um local específico seja de 0,25.(a)
Volte para o Exercício de revisão 5.99(a). Recalcule a probabilidade usando a distribuição binomial.Comente.
O Departamento de Defesa e a tecnologia antimíssil nos fazem ter certeza de que poderemos detectara chegada de projéteis ou mísseis. Para tornar a defesaeficaz, são necessárias múltiplas telas de rada