Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 2.Exercícios - Ex. 8

Para o espaço amostrai do Exercício 2.4:

(a) Liste os elementos correspondentes ao evento A, cuja soma seja maior que 8.

(b) Liste os elementos correspondentes ao evento B, em que ocorra o 2 em qualquer um dos dados.

(c) Liste os elementos correspondentes ao evento C, em que um número maior que 4 seja o resultado no dado verde.

(d) Liste os elementos correspondentes ao evento A ∩ C .

(e) Liste os elementos correspondentes ao evento A ∩ B .

(f) Liste os elementos correspondentes ao evento B ∩ C .

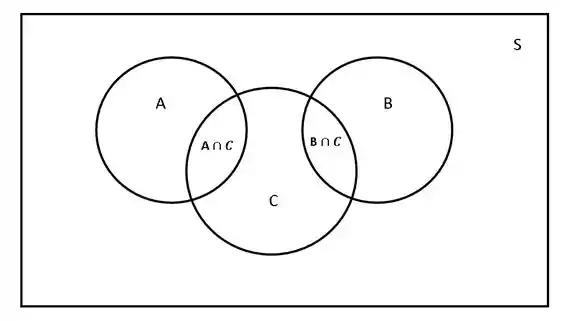
(g) Construa um diagrama de Venn para ilustrar as intersecções e uniões entre os eventos A, B e C.

Passo 1

Falaa, meu querido/minha querida. O experimento do exercício 2.4 O experimento consiste em lançar dois dados, onde x representa o dado verde e y o dado vermelho, cada dado pode ocupar 6 posições diferentes. Sendo assim, nós encontramos o seguinte espaço amostral:

S = { 1 ,   1 ,   1 ,   2 ,   1 ,   3 ,   1 ,   4 ,   1 ,   5 ,   1 ,   6 ,   2 ,   1 ,   2 ,   2 ,   2 ,   3 ,   2 ,   4 ,   2 ,   5 ,   2 ,   6 ,  

3 ,   1 ,   3 ,   2 ,   3 ,   3 ,   3 ,   4 ,   3 ,   5 ,   3 ,   6 ,   4 ,   1 ,   4 ,   2 ,   4 ,   3 ,   4 ,   4 ,   4 ,   5 ,   4 ,   6 ,  

5 ,   1 ,   5 ,   2 ,   5 ,   3 ,   5 ,   4 ,   5 ,   5 ,   5 ,   6 ,   6 ,   1 ,   6 ,   2 ,   6 ,   3 ,   6 ,   4 ,   6 ,   5 ,   6 ,   6 ,   }

Então, bora lá encontrar os eventos que o enunciado nos pede!!!

Passo 2

O enunciado nos pede que o evento A tenha a soma dos dois resultados maior do que 8 . Logo, o evento é:

A = { 3 ,   6 ,   4 ,   5 ,   4 ,   6 ,   5 ,   4 ,   5 ,   5 ,   5 ,   6 ,   6 ,   3 ,   6 ,   4 ,   6 ,   5 ,   6 ,   6 }

Passo 3

Para que ocorra 2 em qualquer um dos resultados do dado, o evento é o seguinte:

B = { 1 ,   2 ,   2 ,   2 ,   3 ,   2 ,   4 ,   2 ,   5 ,   2 ,   6 ,   2 ,   2 ,   1 ,   2 ,   3 ,   2 ,   4 ,   2 ,   5 ,   2 ,   6 }

Passo 4

Como definimos no exercício 2.4, o dado verde é representado pela variável x . Então, o evento solicitado é descrito abaixo:

C = { 5 ,   1 ,   5 ,   2 ,   5 ,   3 ,   5 ,   4 , 5 ,   5 ,   5 ,   6 ,   6 ,   1 ,   6 ,   2 ,   6 ,   3 ,   6 ,   4 ,   6 ,   5 ,   6 ,   6 }

Passo 5

O evento A ∩ C é a intersecção dos dois eventos descritos nos passos anteriores, ou seja, onde acontece os mesmos resultados nos dois eventos.

A ∩ C = { 5 ,   4 ,   5 ,   5 ,   5 ,   6 ,   6 ,   3 ,   6 ,   4 , 6 ,   5 ,   6 ,   6 }

Passo 6

Da mesma forma que no passo 5, o evento A ∩ B é a intersecção desses dois eventos. Porém, neste caso não temos nenhum evento que coincide. Logo:

A ∩ B = ∅

Passo 7

Quase terminando!! A intersecção entre B ∩ C são dois eventos, sendo os seguintes:

  B ∩ C = { 5 ,   2 ,   6 ,   2 }

Passo 8

O diagrama pode ser analisado abaixo, onde o retângulo representa todo o espaço amostral, perceba que não há nenhum ponto de intersecção entra A e B , como calculamos acima.

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

Uma urna contém n bolas vermelhas em bolas azuis. Elas são retiradas uma de cada vez até que um total de r , r ≤ n , bolas vermelhas tenha sido retirado. Determine a probabilidade de que um total de k
Determine a expressão mais simples para os seguintes eventos: (a) ( EUF ) ( EUF C ) ; (b) ( EUF ) ( E CUF ) ( EUF C ) ; (C) ( EUF ) ( FUG )
Demonstre a desigualdade de Boole:P (uuu_(i = 1)^(oo) A_i) = sum_(i = 1)^(oo) P ( A_i )
Mostre que se P (A_i) = 1 para todo i = 1 , então P (nnn_(i = 1)^(oo) A_i) = 1 .
De um grupo de 3 calouros, 4 alunos do segundo ano, 4 alunos do terceiro ano e 3 formandos, forma-se aleatoriamente um comitê de 4 pessoas. Determine a probabilidade de que o comitê seja formado por 1