Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 14.Exercícios - Ex. 8
Há qualquer indicação de que os fatores afetam a taxa de crescimento da fratura? Há qualquer indicação de interação? Use
Analise os residuos desse experimento.
Repita a análise do item , usando como resposta. Analise os residuos dessa nova variável de resposta e comente os seus resultados.
Passo 1
Bom galera, podemos montar uma tabela com os fatores estudados e fica:
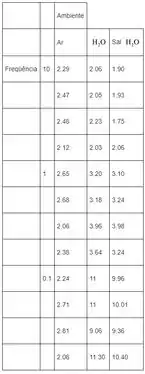
E o modelo é:
As hipóteses devem ser testadas da seguinte forma:
Efeito da frequencia:
Efeito do ambiente:
Interação:
Passo 2
Belezinha, montamos a tabela do Minitab colocando os valores do experimento, assim:
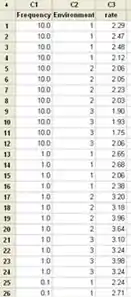
Passo 3
Então, agora fazemos o ANOVA pelo Minitab, e temos como resultado:
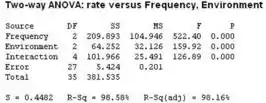
Com isso, observamos que o valor da frequencia é que é menor do que o nível de significância . Portando, rejeitamos a hipótese nula e concluímos que a frequencia afeta a variável resposta.
Da mesma forma temos que o valor do ambiente é que é inferior á . Portanto, rejeitamos a hipótese nula e concluímos que o ambiente afeta a variável resposta.
E o valor da interação é que é menor do que o nível de significância . Assim, podemos rejeitar a hipótese nula e concluímos que há interação significativa entre os dois fatores.
Passo 4
Agora, plotamos os gráficos de probabilidade normal e de resíduos pelo Minitab:
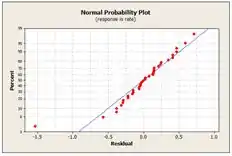
Na primeira temos o gráfico de probabilidade normal dos resíduos. Esse gráfico tem uma leve cauda que não cae exatamente ao longo de uma linha reta, indicando que há alguns problemas com a suposição de normalidade.
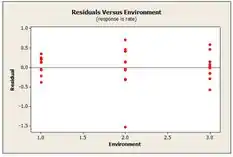
Na segunda e terceira temos os gráficos de resíduos versus dos fatores da frequencia e do ambiente, respectivamente. A frequencia de tem menor variabilidade e o ambiente com tem maior variabilidade dentro do estudo de cada fator.
E na ultima temos os gráfico de resíduos versus valor ajustado, que mostra os resíduos mais elevados a medida que o valor resposa aumenta, isso sugere que deve haver alguma transformação da variável resposta.
Passo 5
Ao usar o minitab na parte esperamos a resposta selecionada como , a analise de variância para fica:
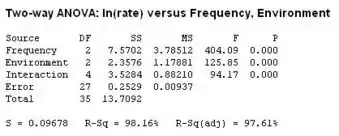
Com isso, observamos que o valor da frequencia é que é menor do que o nível de significância . Portando, rejeitamos a hipótese nula e concluímos que a frequencia afeta a variável resposta.
Da mesma forma temos que o valor do ambiente é que é inferior á . Portanto, rejeitamos a hipótese nula e concluímos que o ambiente afeta a variável resposta.
E o valor da interação é que é menor do que o nível de significância . Assim, podemos rejeitar a hipótese nula e concluímos que há interação significativa entre os dois fatores.
Agora, usando na parte temos:
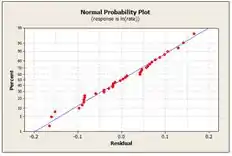
Na primera representa a probabilidade normal dos resíduos, esse gráfico mostra uma linha reta passando pelo centro indicando que os resíduos são normalmente distribuídos.
Na segunda e na terceira temos os gráficos do resíduo versus da frequencia e do ambiente, respectivamente. Nele notamos que o nível de frequencia tem a menor variabilidade e todos os três ambiente fornecem uma variabilidade semelhamente na taxa de fadiga.
Na ultima dos resíduos após a transformação da taxa variável de respota reduz a dispersão.
Resposta
Ei, a resposta está no passo a passo :)