Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 4.4 - Ex. 17
Estatísticas obtidas junto às assistências técnicas indicam que a bomba de água de uma certa lavadora só pode apresentar defeitos após anos de uso. Admita que nos próximos meses, após esse tempo, um mal funcionam e tem probabilidade de ocorrer e, caso ocorra, terá de probabilidade de ser recuperável. O reparo, que só pode ser feito uma vez, tem o preço de enquanto uma bomba nova custa Determine a média e a variância
gasto com essa peça em anos de uso.
Passo 1
Eai,tudo bem? Bora resolver mais um exercício?
Antes de começarmos, vamos construir uma árvore de probabilidade e a tabela da função de probabilidade da variável gasto com a peça em anos de uso. Belezinha?
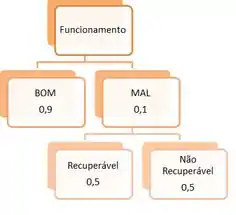
Passo 2
E calculando a esperança (média), temos que:
Calculando
E calculando a variância, por fim, temos que:
Resposta
Logo, concluímos o que nos foi pedido no enunciado.