Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 4.2 - Ex. 5
Para cada item abaixo, construa uma variável aleatória que atenda as condições indicadas.
Passo 1
Vamos lá, nesse exercício temos liberdade para criar.
Em (a), queremos uma v.a que tenha sua média igual a sua moda e igual a sua mediana. Assim, vamos construir nossa v.a:
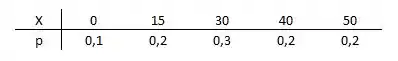
Observe que essa v.a criada atenderá os critérios, pois:
Passo 2
Para (b), temos que construir uma v.a que possua a mediana e a moda iguais, porém, a média tem de ser maior que as duas, assim:
Note que essa nova v.a também atenderá aos critérios, observe:
Passo 3
E finalmente chegamos no último caso!! Temos que criar uma v.a em que a moda seja maior que a mediana, e que a mediana seja maior que a média, daí:
Verificando se a v.a está de acordo com as condições, temos:
Assim, temos a moda maior que a mediana, e a mediana maior que a média.
Resposta
Ei, a resposta está no passo a passo :)