Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.3 - Ex. 1e
Supondo encontre tal que:
(e) com
Passo 1
O último grazadeu!
Então, dessa vez teremos algo muito parecido com o que fizemos anteriormente da um look.
Passo 2
Teremos o seguinte:
Ou seja, temos que buscar na tabela de distribuição de . Maaass lembra que essa tabela é quase um mito??
É muito difícil ter ela; se você tiver este livro em mãos, ta safe demais, só abrir ai na ultima pagina que a tabela estará lindona lá pra você.
Agora, você não ta com o livro ai agora?? Não tem problema, vamos burlar as regras...
Passo 3
Existe uma propriedade da tabela que é mais usada quando você precisa da cauda inferior, porque se você se lembrar, a tabela só trabalha com a cauda superior; mas talvez possamos trazer essa regrinha pra cá e encontrar o que queremos:
Ela diz o seguinte:
Note que aquela mudança entre e no denominador é proposital é extremamente importante.
Trazendo isso pro nossa questão:
Mas o que isso significa?? Que precisamos ir na tabela na coluna de 40 graus de liberdade e na linha de 30:
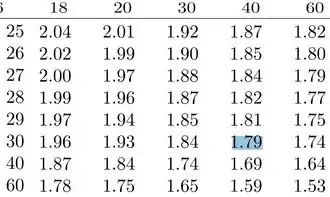
Encontramos o seguinte:
Mas ainda não é isso que a gente quer, não esquece..
Portanto,
com
Resposta
Concluimos que quando tomamos 30 e 40 graus de liberdade.