Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.3 - Ex. 1d
Supondo encontre tal que:
(d) com
Passo 1
Bom, tamo quase terminando por aqui, você já deve ter pegado o jeito né?!
Então tá; bom, pela milésima vez temos novamente que procurar na tabela de distribuição .
Passo 2
Só que dessa vez temos uma probreminha... olha só:
Isso significa que temos de buscar na tabela de . Essa tabela é muito difícil de termos em mãos, eu por exemplo não tenho.
Mas como pra tudo na vida tem um jeito, podemos utilizar de uma propriedade da tabela para encontrar mais ou menos o que queremos. Olha só:
Percebeu o que aconteceu?? Invertemos os graus de liberdade ali no denominador; trazendo isso pro nosso exercício, teremos o seguinte:
Passo 3
Portanto, basta buscarmos na tabela olhando na coluna de 12 graus de liberdade e na linha de 5 graus livres:
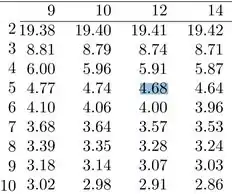
Com isso, encontramos:
Portanto:
Podemos concluir que:
com e .
Resposta
Concluimos então, que quando tivermos 12 e 5 graus de liberdade.